Question

Let f(x)=4x² +16x+21 a) Find the vertex of f b) Write in the form f(x)= a(x-h)² +k

Answer 1

see explanation

Explanation:

given a parabola in standard form

f(x) = ax² + bx + c ( a ≠ 0 )

then the x- coordinate of the vertex is

`x_(vertex)` = -
`(b)/(2a)`

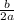
f(x) = 4x² + 16x + 21 ← is in standard form

with a = 4 , b = 16 , then

`x_(vertex)` = -
`(16)/(8)` = - 2

for corresponding y- coordinate substitute x = - 2 into f(x)

f(- 2) = 4(- 2)² + 16(- 2) + 21

= 4(4) - 32 + 21

= 16 - 11

= 5

vertex = (- 2, 5 )

the vertex = (h, k ) = (- 2, 5 ) , then

f(x) = a(x - (- 2) )² + 5

= a(x + 2)² + 5

here a = 4 , then

f(x) = 4(x + 2)² + 5 ← in the form a(x - h)² + k