Question

Use the given conditions to write an equation for the line in standard form Passing through (-6,-2) and parallel to the line whose equation is y - 6 = 1/2 (x-3) Write an equation for the line in standard form. (Type your answer in standard form, using integer coefficients with A≥0.)

Answer 1

Hello !

Answer:

`\Large \boxed{\sf x-2y=-2}`

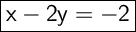
Explanation:

- The slope-intercept form of a line is of the form y=mx+b where m is the slope and b is the y-intercept.

- The standard form is Ax+By=C where A,B and C are integers.

We know that the line :

• is parallel to the line whose equation is
  `\sf y-6=(1)/(2)(x-3)`
• passes through (-6,-2)

Let's put
`\sf y-6=(1)/(2)(x-3)` in the slope-intercept form.

Expand right side :

`\sf y-6=(1)/(2)x-(3)/(2)`

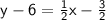
Add 6 to both sides to isolate y :

`\sf y=(1)/(2) x+(9)/(2)`

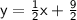
The two lines are parallel and therefore have the same slope :
`\sf (1)/(2)`

We have
`\sf y=(1)/(2) x+b`.

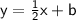We know that the lines passes through (-6,-2).

Let's replace x and y with -6 and -2 and solve for b :

`\sf -2=(1)/(2) (-6)+b\\\iff -2=-3+b\\ \iff b=1`

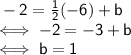
The slope-intercept form our line is
`\sf y=(1)/(2) x+1`.

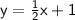Let's put it into standard form :

Multiply both sides by 2 :

`\sf 2y=x+2`

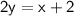
Substract 2y from both sides :

`\sf 0=x-2y+2`

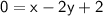
Finally, substract 2 from both sides :

`\boxed{\sf x-2y=-2}`

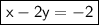
Have a nice day ;)