Question

Please help! mathematicians

Answer 1

1 < m < 4

Explanation:

If the roots of function f(x) are not real, then the discriminant (the part under the square root sign) will be negative.

Set the discriminant less than zero and rewrite in standard form:

`\begin{aligned}16-4m(-m+5)& < 0\\16+4m^2-20m& < 0\\4m^2-20m+16& < 0\\4(m^2-5m+4)& < 0\\m^2-5m+4& < 0\end{aligned}`

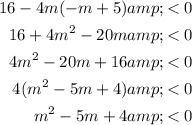
Factor the quadratic:

`\begin{aligned}m^2-5m+4& < 0\\m^2-4m-m+4& < 0\\m(m-4)-1(m-4)& < 0\\(m-1)(m-4)& < 0\end{aligned}`

The leading coefficient of the quadratic m² - 5m + 4 is positive.

Therefore, the graph will be a parabola that opens upwards.

This means that the interval where the parabola is below the x-axis (negative) is between the zeros of the quadratic. Since the zeros are m = 1 and m = 4, the solution to the inequality is 1 < m < 4.

Therefore, the values of m for which the roots of function f(x) will be non-real are 1 < m < 4.