Question

Please help!
mathematics question

Answer 1

k = 6 and k = -4

Explanation:

To determine two integral values of k (integer values of k) for which the roots of the quadratic equation kx² - 5x - 1 = 0 will be rational, we can use the Rational Root Theorem.

The Rational Root Theorem states that if a rational number p/q is a root of a polynomial equation with integer coefficients, then p must be a factor of the constant term (in this case, -1) and q must be a factor of the leading coefficient (in this case, k).

Possible p-values:

• Factors of the constant term: ±1

Possible q-values:

• Factors of the leading coefficient: ±1, ±k

Therefore, all the possible values of p/q are:

`\sf (p)/(q)=(\pm 1)/(\pm 1), (\pm 1)/(\pm k)=\pm 1, \pm (1)/(k)`

To find the integral values of k, we need to check the possible combinations of factors. Substitute each possible rational root into the function:

`\begin{aligned} x=1 \implies k(1)^2-5(1)-1 &= 0 \\k-6 &= 0 \\k&=6\end{aligned}`

`\begin{aligned} x=-1 \implies k(-1)^2-5(-1)-1 &= 0 \\k+4 &= 0 \\k&=-4\end{aligned}`

`\begin{aligned} x=(1)/(k) \implies k\left((1)/(k) \right)^2-5\left((1)/(k) \right)-1 &= 0 \\(1)/(k)-(5)/(k)-1 &= 0 \\-(4)/(k)&=1\\k&=-4\end{aligned}`

`\begin{aligned} x=-(1)/(k) \implies k\left(-(1)/(k) \right)^2-5\left(-(1)/(k) \right)-1 &= 0 \\(1)/(k)+(5)/(k)-1 &= 0 \\(6)/(k)&=1\\k&=6\end{aligned}`

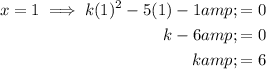
Therefore, the two integral values of k for which the roots of the equation kx² - 5x - 1 = 0 will be rational are k = 6 and k = -4.

Note:

If k = 6, the roots are 1 and -1/6.

If k = -4, the roots are -1 and -1/4.