Question

NO LINKS!! URGENT HELP PLEASE!!

Find the probability of each event.

28. One day, 9 babies are born at a hospital. Assuming each baby has an equal chance of being a boy or girl, what is the probability that exactly 4 of the 9 babies are girls?

29. A gambler places a bet on a horse race. To win, he must pick the top 3 finishers in order. 13 horses of equal ability are entered in the race. Assuming the horses finish in random order, what is the probability that the gambler will win his bet?

Answer 1

28) 0.246 = 24.6%

29) 1/286 = 0.350%

Explanation:

Question 28

We can model the given scenario as a binomial distribution.

Binomial distribution

`X \sim \text{B}(n,p)`

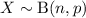
where:

• X is the random variable that represents the number of successes.
• n is the fixed number of independent trials.
• p is the probability of success in each trial.

Given the probability that a baby is born a girl is 0.5, and the number of babies is 9:

`\boxed{X \sim \text{B}(9,0.5)}`

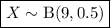
where the random variable X represents the number of babies who are girls.

To find the probability that at exactly 4 babies are girls, we need to find P(X = 4).

To do this, we can use the binomial distribution formula:

`\boxed{\displaystyle \text{P}(X=x)=\binom{n}{x} \cdot p^x \cdot (1-p)^(n-x)}`

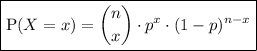
Substitute the values of n = 9, p = 0.5 and x = 4 into the formula:

`\begin{aligned}\displaystyle \text{P}(X=4)&=\binom{9}{4} \cdot 0.5^4 \cdot (1-0.5)^(9-4)\\\\&=(9!)/(4!\:(9-4)!) \cdot 0.5^4 \cdot 0.5^(5)\\\\&=126 \cdot 0.0625 \cdot 0.03125\\\\& = 0.24609375\end{aligned}`

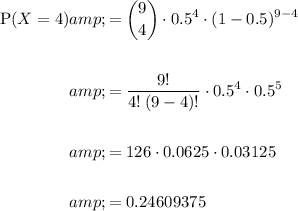
Therefore, the probability that 4 babies from a sample of 9 babies are girls is 0.246 (3 s.f.) or 24.6%.

We can also use the binomial probability density function of a calculator to calculate P(X = 4).

Inputting the values of n = 9, p = 0.5 and x = 4 into the binomial pdf:

`\text{P}(X=4)=0.24609375`

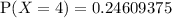
Therefore, this confirms that the probability that 4 babies from a sample of 9 babies are girls is 0.246 (3 s.f.) or 24.6%.

`\hrulefill`

Question 29

To calculate the probability that the gambler will win his bet, we need to determine the number of favorable outcomes (winning combinations) and the total number of possible outcomes.

The gambler wins if he picks the top three horses in any order. There are 6 ways for the three winners to be arranged in the top three.

There are a total of 13 horses in the race.

• The number of ways to choose the first-place horse is 13.
• After the first-place horse is chosen, there are 12 remaining horses, so the number of ways to choose the second-place horse is 12.
• Finally, after the first two horses are chosen, there are 11 remaining horses, so the number of ways to choose the third-place horse is 11.

Therefore, the total number of possible outcomes is:

`13 * 12 * 11 = 1716`

Therefore, the probability that the gambler will win his bet is:

`\begin{aligned} \sf Probability &=\sf (Favorable \;outcomes)/(Total\;outcomes)\\\\&=(6)/(1716)\\\\&=(1)/(286)\\\\ & \approx0.350\%\; \sf (3\;d.p.)\end{aligned}`

Answer 2

28. 0.2461 or 24.61%.

29. 0.00058275 or 0.058275%.

Explanation:

Question 28:

we can use the binomial probability formula to calculate the probability:

`\boxed{\bold{P(X = k) = (nCk) * p^k * (1 - p)^(n - k)}}`

Where:

• P(X = k) is the probability of getting exactly k successes
• nCk is the number of combinations of n items taken k at a time
• p is the probability of a single success

• n is the total number of trials

In this case, we have n = 9 babies, and each baby has a 50% chance of being a girl (p = 0.5). We want to find the probability that exactly 4 of them are girls (k = 4).

Using the formula, we can calculate the probability as follows:

`\bold{P(X = 4) = (9C4) * (0.5)^4 * (1 - 0.5)^(9 - 4)}`

Calculating the values:

• (9C4) = 126
• (0.5)^4 = 0.0625
• (1 - 0.5)^(9 - 4) = 0.5^5 = 0.03125

Now, we can substitute these values into the formula:

P(X = 4) = 126 * 0.0625 * 0.03125 = 0.2461 or 24.61%

Therefore, the probability that exactly 4 out of 9 babies are girls is approximately 0.2461 or 24.61%.

Question 29:

We need to calculate the number of possible outcomes to calculate this probability, where the gambler correctly predicts the top 3 finishers in order and divides it by the total number of possible outcomes.

The total number of possible outcomes is the number of permutations of 13 horses taken 3 at a time.

This can be calculated as:

`13P3 = (13! )/((13 - 3)! )= (13! )/( 10! )=(13*12*11*10! )/( 10! )= 13 * 12 * 11 = 1,716`

Now,

To calculate the number of favorable outcomes where the gambler predicts the top 3 finishers correctly, we need to consider that there is only one correct order for the horses to finish.

Therefore, there is only one favorable outcome.

The probability of the gambler winning his bet is given by:

`\boxed{\bold{P\:(winning) = (Number\: of \:favorable\: outcomes )/( Total \:number \:of \:outcomes)}}`

`P(winning) = (1 )/(1,716)=0,00058275 \: or\:0.058275%`

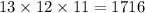
Therefore, the probability that the gambler will win his bet is approximately 0.00058275 or 0.058275%.