Question

A certain radioactive substance decays by 2.9% each year. Find the half-life of the substance, to 2 decimal places.

How many in years?

Answer 1

23.90 years

Explanation:

To find the half-life of a radioactive substance, we can use the formula:

`\boxed{\begin{minipage}{10 cm}\underline{Half-life formula}\\\\$ t_(1/2) =(\ln 2)/(k)$\\\\where:\\\\ \phantom{ww}$\bullet$ $t_(1/2)$ is the half-life. \\ \phantom{ww}$\bullet$ $k$ is the decay constant (percentage decay rate per year)\\ \end{minipage}}`

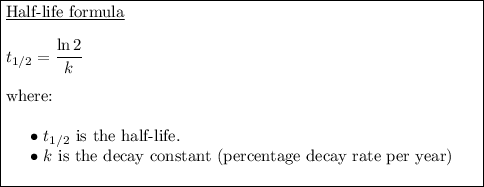
In this case, the decay constant is 2.9% or 0.029 (expressed as a decimal). Therefore, substitute k = 0.029 into the formula:

`t_(1/2) =(\ln 2)/(0.029)`

`t_(1/2) =23.9016269...`

`t_(1/2) =23.90\; \sf years\; (2\;d.p.)`

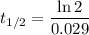
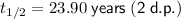
Therefore, the half-life of the radioactive substance, rounded to 2 decimal places, is approximately 23.90 years.