Question

Find the 12th term of the geometric sequence 10, -50, 250, ...

Answer 1

Answer: -488,281,250

Step-by-step explanation:

The starting term is a = 10.

The common ratio r is found by dividing each term by its previous term.

• r = (term2)/(term1) = -50/10 = -5
• r = (term3)/(term2) = 250/(-50) = -5

The nth term is therefore
`a_n = a(r)^(n-1) = 10(-5)^(n-1)`

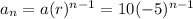
Plug in n = 12 to get the 12th term:

`a_n = 10(-5)^(n-1)\\\\a_(12) = 10(-5)^(12-1)\\\\a_(12) = 10(-5)^(11)\\\\a_(12) = 10(-48,828,125)\\\\a_(12) = -488,281,250\\\\`

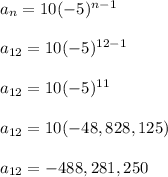
Delete the commas if your teacher requires it.