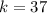Question

50 POINTS TO BEST ANSWER

A function is shown below where b is a real number.
f(x)=x²+bx+118
The minimum of the function is 37.
Create an equivalent equation of the function in the form f(x)=(x-h)²+k.
Type your numerical answers below for h and k. Use the hyphen (-) for the negative sign if
necessary.
h=
k=

Answer 1

I did some research and found that for quadratic equations in the form of
`y = ax^2 + bx + c`, you can find the minimum value using the equation
`$\text{minimum} = c - (b^2)/(4a)` .

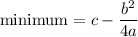We can substitute our given values in the formula and get the following:
`$37 = 118 - (b^2)/(4)$` .

We can go ahead and solve it, and get the following:

`-81 = -(b^(2))/(4)`

`324 = b^2`

`\pm{18} = b`

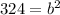
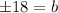
Now we know that the equation is either
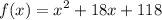`$f(x)=x^2+18x+118$` or
`$f(x)=x^2-18x+118$` .

We will solve using both equations, but we will solve the one with a positive b-value first. Substituting
`f(x)` for
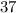`$37$`, the minimum or y-value of the vertex, we can now solve for the x-value of the vertex.

We have:

`37 = x^2+18x+118`

`0=x^2+18x+81`

`0=(x+9)^2`

`x+9=0\\x=-9`

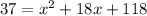
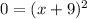
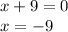
Doing the same thing with the second equation, we get:

`37 = x^2-18x+118`

`0=x^2-18x+81`

`0=(x-9)^2`

`x-9=0\\x=9`

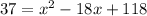
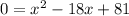
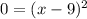
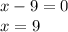
After all of this, we know our vertex's x-values are either
`9` or
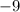`-9`, and that our y-value is
`37\\`.

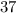We can conclude that our k-value (y-value of the vertex in vertex form) is
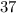`37`, and our h-value (x-value of the vertex in vertex form) is
`9` or
`-9`.

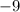Conclusion:
`h = -9, 9`

`k=37`