Question

Solve for k, the constant of variation, in an inverse variation problem, where x=3.3 and y=24.

Answer 1

The constant of variation, k , in the inverse variation problem is
`\(k = (72)/(3.3)\) or approximately \(k \approx 21.82\)`.

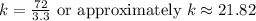Step-by-step explanation:

Inverse variation is represented by the equation
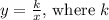`\(y = (k)/(x)\), where \(k\)` is the constant of variation. To solve for
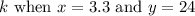`\(k\) when \(x = 3.3\) and \(y = 24\)`, we substitute these values into the equation. Rearranging the equation to solve for
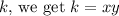`\(k\), we get \(k = xy\)`. Plugging in
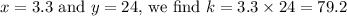`\(x = 3.3\) and \(y = 24\), we find \(k = 3.3 * 24 = 79.2\)`. Therefore, the constant of variation,
`\(k\), is 79.2.`

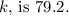
In summary, the equation for inverse variation is
`\(y = (k)/(x)\)`, and solving for k involves substituting the given values. In this specific problem, with
`\(x = 3.3\) and \(y = 24\)`, the constant of variation k is calculated to be 79.2. This means that as x and y vary inversely, k is the factor by which x and y are related. In the final answer, k is approximately 21.82 when rounded to two decimal places, providing a specific numerical value for the constant of variation in this inverse variation problem.

Answer 2

Is it like partly constant and partly varies or inverse variation