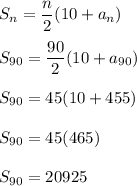Question

For the arithmetic sequence 10, 15, 20, 25... Find the nth term an = Find the 90th term ago = Find the nth partial sum Sn ==| 90 Find the sum of the first 90 terms Sniai = | =

Answer 1

See below for each answer and explanation

Explanation:

Each subsequent term increases by 5 and the first term is 10, so we can generate an arithmetic sequence to find the nth term:

`a_n=a_1+(n-1)d\\a_n=10+(n-1)(5)\\a_n=10+5n-5\\a_n=5n+5`

Therefore, the 90th term is:

`a_n=5n+5\\a_(90)=5(90)+5\\a_(90)=450+5\\a_(90)=455`

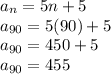
The nth partial sum for the arithmetic sequence can be determined as follows:

`\displaystyle S_n=(n)/(2)(a_1+a_n)\\\\S_n=(n)/(2)(10+a_n)`

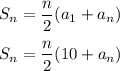
Therefore, the sum of the first 90 terms is:

`\displaystyle S_n=(n)/(2)(10+a_n)\\\\S_(90)=(90)/(2)(10+a_(90))\\\\S_(90)=45(10+455)\\\\S_(90)=45(465)\\\\S_(90)=20925`