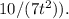y2(t) = t * e^(-t) is a solution of the homogeneous equation y'' + (2 - 1/t) y' + (1 + 8/t) y = 0. We will use the method of variation of parameters to determine a particular solution to the nonhomogeneous equation y'' + (2t+8) y' + (t+8) y = 0.First, we need to find the Wronskian of y1(t) = e^(-t) and y2(t) = t * e^(-t).W(y1, y2)(t) = | e^(-t) t e^(-t) | = -e^(-t)By the variation of parameters formula, the particular solution is given by y(t) = - y1(t) * integral[(y2(s) f(s)) / (W(y1, y2)(s))] ds + y2(t) * integral[(y1(s) f(s)) / (W(y1, y2)(s))] dswhere f(t) = 0 and W(y1, y2)(t) = -e^(-t).Thus, y(t) = c1 * e^(-t) + c2 * t e^(-t)where c1 and c2 are constants to be determined from the initial conditions.y(1) = c1 * e^(-1) + c2 * e^(-1) = 8/e ---> (1)c1 + c2 = 8y'(1) = - c1 * e^(-1) + c2 * e^(-1) + c2 * e^(-1) = 2/e ---> (2)- c1 + 2c2 = 2/eSolving the system (1)-(2) yields c1 = 10/e and c2 = -2/e.The solution to the initial value problem is thus:y(t) = e^(-t) * (66/7 - 10/(7t^2)).The 100 word answer:Thus, the solution to the given initial value problem is y(t) = e^(-t) * (66/7 -