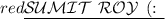Part A:
To find the linear form of vector u=ST, we subtract the coordinates of the initial point S from the coordinates of the terminal point T:
u = T - S
u = (5, 19) - (14, 23)
u = (-9, -4)
Therefore, the linear form of vector u is u = -9i - 4j.
Part B:
To find 4u - 5v, we first need to find the linear forms of vectors u and v.
u = -9i - 4j
v = B - A
v = (32, 9) - (7, 17)
v = (25, -8)
Now we can calculate 4u - 5v:
4u - 5v = 4(-9i - 4j) - 5(25i - 8j)
4u - 5v = (-36i - 16j) - (125i - 40j)
4u - 5v = -36i - 16j - 125i + 40j
4u - 5v = (-36i - 125i) + (-16j + 40j)
4u - 5v = -161i + 24j
Therefore, 4u - 5v is equal to -161i + 24j.
Part C:
To determine if vectors t and u are parallel, orthogonal, or neither, we can use the dot product. The dot product of two vectors is given by the formula:
t · u = t1u1 + t2u2
Given vector 1 = -161 + 36j and vector u = -9i - 4j, we can calculate the dot product:
t · u = (-161)(-9) + (36)(-4)
t · u = 1449 - 144
t · u = 1305
Since the dot product is not equal to zero, vectors t and u are not orthogonal.
Part D:
To find another vector w that has the same relationship to vector t as vector u, we can use the concept of scalar multiplication. If we multiply vector t by a scalar value, we can obtain vector w.
Let's choose a scalar value of 3. We can calculate w as:
w = 3t
w = 3(-161i + 36j)
w = -483i + 108j
Therefore, vector w = -483i + 108j has the same relationship to vector t as vector u.

♥️