Question

find the solution of the differential equation that satisfies the given initial condition. dy dx = 5xey, y(0) = 0

Answer 1

To solve the differential equation dy/dx = 5x e^y with the initial condition y(0) = 0, use separation of variables and integration to find y = -ln((5/2)x^2 - 1).

Step-by-step explanation:

The solution to the differential equation dy/dx = 5x ey, which satisfies the initial condition y(0) = 0, can be found using the method of separation of variables. We can rewrite the equation as dy/ey = 5x dx. Integrating both sides gives us ∫ dy/ey = ∫ 5x dx, leading to -e-y = (5/2)x2 + C. Using the initial condition, we substitute x = 0 and y = 0 to find the constant C, which gives us C = -1. Consequently, the solution is e-y = (5/2)x2 - 1 or y = -ln((5/2)x2 - 1).

Answer 2

The solution to the differential equation
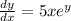`\((dy)/(dx) = 5xe^y\)` with the initial condition y(0) = 0 is
`\(y = \ln(1 + (5x^2)/(2))\)`.

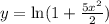Step-by-step explanation:

To solve the differential equation
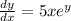`\((dy)/(dx) = 5xe^y\)` with the initial condition y(0) = 0, we start by separating variables. Rearrange the equation to isolate y terms on one side and x terms on the other side:

`\((dy)/(e^y) = 5x \,dx\)`

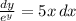
Integrate both sides of the equation with respect to their respective variables:

`\(\int (1)/(e^y) \,dy = \int 5x \,dx\)`

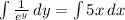
The left-hand side integral simplifies to
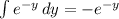`\(\int e^(-y) \,dy = -e^(-y)\)`. The right-hand side integral is
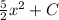`\((5)/(2)x^2 + C\)`, where C is the constant of integration.

Therefore, after integrating both sides and considering the initial condition y(0) = 0, we solve for the constant C using the initial condition: 0 = -1 + C, which implies that C = 1.

Finally, solving for y yields
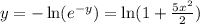`\(y = -\ln(e^(-y)) = \ln(1 + (5x^2)/(2))\)`, which satisfies the given differential equation with the initial condition y(0) = 0.