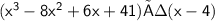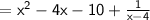What is (x³-8x² + 6x +41) ÷ (x-4)

Question

asked Jul 28, 2024 142k views

1 Answer

Alejandro Quintanar · Answer 1 · 2024-08-03T19:23:06+0000

Step 1: Write the dividend and divisor:

$\sf\:\frac{{x^3 - 8x^2 + 6x + 41}}{{x - 4}} \\$

Step 2: Divide the first term of the dividend by the first term of the divisor:

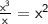
$\sf\:\frac{{x^3}}{{x}} = x^2 \\$

Step 3: Multiply the divisor (x - 4) by the result (x^2):

$\sf\:(x - 4) \cdot (x^2) = x^3 - 4x^2 \\$

Step 4: Subtract the result from the original dividend:

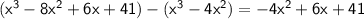
$\sf\:(x^3 - 8x^2 + 6x + 41) - (x^3 - 4x^2) = -4x^2 + 6x + 41 \\$

Step 5: Bring down the next term from the dividend:

$\sf\:\frac{{-4x^2 + 6x + 41}}{{x - 4}} \\$

Step 6: Repeat steps 2-5 with the new dividend:

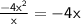
$\sf\:\frac{{-4x^2}}{{x}} = -4x \\$

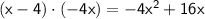
$\sf\:(x - 4) \cdot (-4x) = -4x^2 + 16x \\$

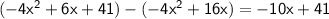
$\sf\:(-4x^2 + 6x + 41) - (-4x^2 + 16x) = -10x + 41 \\$

Step 7: Bring down the next term from the dividend:

$\sf\:\frac{{-10x + 41}}{{x - 4}} \\$

Step 8: Repeat steps 2-5 with the new dividend:

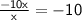
$\sf\:\frac{{-10x}}{{x}} = -10 \\$

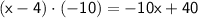
$\sf\:(x - 4) \cdot (-10) = -10x + 40 \\$

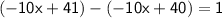
$\sf\:(-10x + 41) - (-10x + 40) = 1 \\$

Step 9: There are no more terms to bring down, so the division is complete.

Step 10: Write the final result:

The quotient is
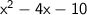$\sf\:x^2 - 4x - 10\\$ and the remainder is 1.

Therefore, the division of
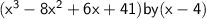$\sf\:(x^3 - 8x^2 + 6x + 41) by (x - 4) \\$ is:

$\sf\:(x^3 - 8x^2 + 6x + 41) ÷ (x - 4) \\$
$\sf\:= x^2 - 4x - 10 + \frac{{1}}{{x - 4}} \\$