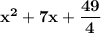Question

What would be the perfect square trinomial for x^{2} +7x

Answer 1

`x^2 + 7x +(49)/(4)`

Explanation:

In this problem, we are asked to find the perfect square trinomial that starts with the expression
`x^2 + 7x`.

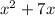We need to find the constant term that would make the expression
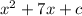`x^2 + 7x + c` a perfect square.

To find this, we can look to the expanded form of a perfect square:

`(x + a)^2 = x^2 + 2a + a^2`

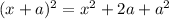
We can see that the constant in the factored form (
`a`) is

1. half of the coefficient of the middle term
2. squared

To get the constant term that would make the expression, we can perform the following operations to the coefficient of the middle term:

`7`

↓ dividing by 2

`(7)/(2)`

↓ squaring

`\frac{49}4`

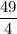
So, the perfect square trinomial that starts with
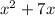`x^2 + 7x` is:

`\bold{x^2 + 7x +(49)/(4)}`