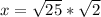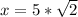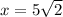Answer:
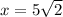
Explanation:
Main concepts
1. Isosceles Triangles
2. Pythagorean theorem
1. Isosceles Triangles
For this triangle to be an isosceles triangle, two sides must be congruent (the same length).
As a consequence, the two angles across from those two congruent sides must be congruent angles (have the same measure).
Our triangle
We are given the hypotenuse (side across from the right angle) is 10, and one side is length x. In order for the triangle to be isosceles, the unlabeled side must either be length x or length 10.
For any triangle, the increasing measure of the angles corresponds with the increasing lengths of the sides across from those angles, meaning that the smallest angle in a triangle always has the smallest side of that triangle as the side across from that smallest angle, and the largest angle of the triangle has the longest side as the side across from that largest angle.
In a right triangle, the right angle is always the largest angle, so the hypotenuse (the side across from the right angle), is always the longest side in a right triangle.
Since the angle across from the unlabeled side cannot also be 90 degrees (if it were, the sum of the angles of the triangle would be more than 180 degrees), the unlabeled side must be length "x"
2. Pythagorean Theorem
For any right triangle, requiring side "c" to be the length of the hypotenuse, and sides a & b to be the other two sides (legs -- the two sides touching the right angle) of the triangle, the lengths of the sides of the right triangle must obey the equation:
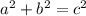
Since, we have determined that the length of both legs is "x", we can substitute the quantities into the equation:
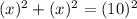
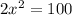
divide both sides by 2...

Apply a square root to both sides...

Factor the radical
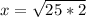
Since the factors are all positive, the radical of a product is the product of radicals...