Question

Let f(x)

(4-x-x²
2x - 1
lim
2+1
Use a graph to determine the following limits. Enter DNE if the limit does not exist.
lim
2-1
f(x) =
f(x)
if x ≤ 1
if x > 1
lim f(x)
z 1

Answer 1

See below for answers and explanations

Explanation:

`\displaystyle \lim_(x\rightarrow1^(-))f(x) = 4-(1)-(1)^2=4-1-1=3-1=2\\\\\lim_(x\rightarrow1^(+))f(x) = 2(1)-1=2-1=1\\\\\lim_(x\rightarrow1)f(x) = DNE`

Note that
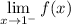`\displaystyle \lim_(x\rightarrow1^-)f(x)` represents the left-side limit (so the limit of f(x) as x approaches 1 from the left), and
`\displaystyle \lim_(x\rightarrow1^+)f(x)` represents the right-side limit (so the limit of f(x) as x approaches 1 from the right)

Because
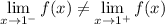`\displaystyle \lim_(x\rightarrow1^-)f(x)\\eq\displaystyle \lim_(x\rightarrow1^+)f(x)`, then
`\displaystyle \lim_(x\rightarrow1)f(x)=DNE`

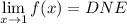
I hope this helped!