Question

The answer to this word problem and the distance needed

Answer 1

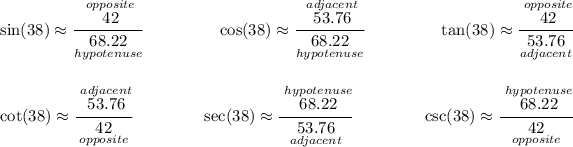
Check the picture below.

`\tan(38^o )=\cfrac{\stackrel{opposite}{42}}{\underset{adjacent}{x}} \implies x=\cfrac{42}{\tan(38^o)}\implies x\approx 53.76 \\\\[-0.35em] ~\dotfill\\\\ \sin( 38^o )=\cfrac{\stackrel{opposite}{42}}{\underset{hypotenuse}{y}} \implies y=\cfrac{42}{\sin(38^o)}\implies y\approx 68.22`

Make sure your calculator is in Degree mode.

now as far as the ∡z goes, well, is really a complementary angle with 38°, so ∡z=52°, and of course the angle at the water level is a right-angle.

By the way, the "y" distance is less than 150 feet, so might as well, let the captain know, he's down below playing bingo.

hmmm let's get the functions for the 38° angle.

`\sin(38 )\approx \cfrac{\stackrel{opposite}{42}}{\underset{hypotenuse}{68.22}}~\hfill \cos(38 )\approx \cfrac{\stackrel{adjacent}{53.76}}{\underset{hypotenuse}{68.22}}~\hfill \tan(38 )\approx \cfrac{\stackrel{opposite}{42}}{\underset{adjacent}{53.76}} \\\\\\ \cot(38 )\approx \cfrac{\stackrel{adjacent}{53.76}}{\underset{opposite}{42}}~\hfill \sec(38 )\approx \cfrac{\stackrel{hypotenuse}{68.22}}{\underset{adjacent}{53.76}}~\hfill \csc(38 )\approx \cfrac{\stackrel{hypotenuse}{68.22}}{\underset{opposite}{42}}`