Question

Y = x² + 6x - 12

a =______
b = _____
c=______
h=______
k =_____
y-intercept=______
x-intercepts =______
and_____

Answer 1

See below for answers and explanations

Explanation:

a, b, and c are the coefficients of the quadratic, so a=1, b=6, and c=-12

(h,k) is the vertex of the parabola, so we must convert it to vertex form by completing the square:

`y=x^2+6x-12\\y+21=x^2+6x-12+21\\y+21=x^2+6x+9\\y+21=(x+3)^2\\y=(x+3)^2-21`

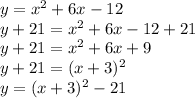
Therefore, the vertex is (3,-21), which means h=-3 and k=-21.

The y-intercept is when x=0, or when the function passes through the x-axis:

`y=x^2+6x-12\\y=0^2+6(0)-12\\y=-12`

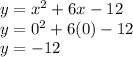
Therefore, the y-intercept is -12 (also written as (0,-12) as an ordered pair).

The x-intercept is when y=0, or when the function passes through the y-axis:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)\\\\x=(-6\pm√(6^2-4(1)(-12)))/(2(1))\\\\x=(-6\pm√(36+48))/(2)\\\\x=(-6\pm√(94))/(2)`

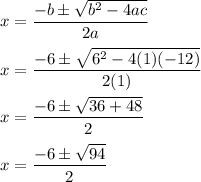
Therefore, the x-intercepts are (-6+√94)/2 and (-6-√94)/2.

Hope this helped!