Question

Help i have a test tomorrow and i don’t know how to do this

Answer 1

Check the picture below.

`\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=√(c^2 - a^2) \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{14.5}\\ a=\stackrel{adjacent}{8}\\ o=\stackrel{opposite}{x} \end{cases} \\\\\\ x=√( 14.5^2 - 8^2)\implies x=√( 210.25 - 64 ) \implies x=√( 146.25 )\implies x\approx 12.09`

Answer 2

The distance from each chord to the center of the circle is approximately 12.09 inches.

Explanation:

To find the distance from each chord to the center of the circle, we can use the following formula:

`d = √(r^2-(l/2)^2)`

Where:

- "d" is the distance from the chord to the center of the circle,

- "r" is the radius of the circle, and

- "l" is the length of the chord.

Given that the diameter of the circle is 29 inches, we can find the radius by dividing the diameter by 2:

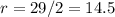`r = 29/2 = 14.5` Inches

Now, let's calculate the distance from each chord to the center of the circle:

For the first chord with a length of 16 inches:

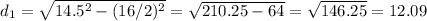`d_(1) =√(14.5^2-(16/2)^2) = √(210.25-64) = √(146.25) = 12.09` Inches

For the second chord with a length of 16 inches:

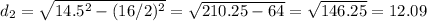`d_(2) = √(14.5^2-(16/2)^2) = √(210.25-64) = √(146.25) = 12.09` Inches

Therefore, the distance from each chord to the center of the circle is approximately 12.09 inches.