Question

PLEASE HELP ME ANSWER THIS QUESTION I REALLY NEED IT

The radius 5cm, of a sphere increases at the rate of 0.4 cm/s. At what rate will the area be increasing?
a) 40 pi cm^2/s b) 24 pi cm^s/ s c) 16 pi cm^2/ s d) 10 pi cm^2/ s

Answer 1

The rate at which the surface area of the sphere is increasing is 16π cm^2/s.(option-c)

To find the rate at which the area of a sphere increases when its radius is increasing at a given rate, we can use the formula for the surface area of a sphere, which is A =
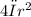`4πr^2`, where r is the radius of the sphere and A is its surface area. We can then differentiate this with respect to time t to find the rate of change of area with respect to time, which is given as dA/dt.

Given that the radius of the sphere increases at the rate of 0.4 cm/s, we can find the rate of change of area as follows:

- Differentiate the surface area formula with respect to time t:

dA/dt = d/dt
`(4πr^2)`

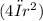
- Use the chain rule to differentiate
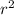`r^2`with respect to time t:

d/dt (r^2) = 2r (dr/dt)

- Substitute the value of dr/dt given as 0.4 cm/s, and the radius value as 5 cm:

dA/dt = 4π(5)^2 (2 × 0.4)

- Simplify the expression to get the rate of change of area with respect to time:

dA/dt = 16π
`cm^2/s`

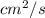
(option-c)