Question

Please help! maths hyperbolic functions

Answer 1

See attachments.

Explanation:

The quickest way to sketch the given functions, given that the coordinate plane is restricted to -5 ≤ x ≤ 5, is to substitute the values of x into the functions to find the points for the given interval. Plot these points on the given coordinate plane, and draw a continuous curve through the points.

Part (a)

Given function:

`y=(5)/(x)-2, \quad x > 0`

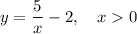
Substitute the values of x = 1, x = 2, x = 3, x = 4 and x = 5 into the function:

`\begin{aligned}x=1 \implies y&=(5)/(1)-2\\&=5-2\\&=3\end{aligned}`

`\begin{aligned}x=2 \implies y&=(5)/(2)-2\\&=2.5-2\\&=0.5\end{aligned}`

`\begin{aligned}x=3 \implies y&=(5)/(3)-2\\&=-0.333...\end{aligned}`

`\begin{aligned}x=4 \implies y&=(5)/(4)-2\\&=1.25-2\\&=-0.75\end{aligned}`

`\begin{aligned}x=5 \implies y&=(5)/(5)-2\\&=1-2\\&=-1\end{aligned}`

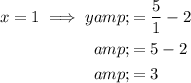
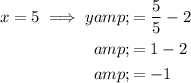
Plot the points (1, 3), (2, 0.5), (3, -0.333...), (4, -0.75) and (5, -1) on the given coordinate plane and draw a continuous curve through them.

End behaviour:

• As x approaches 0 from the positive side, x tends to ∞.
• As x approaches ∞, y approaches -2.

`\hrulefill`

Part (b)

Given function:

`y=(-2)/(x+1)+3, \quad x < -1`

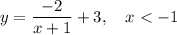
Substitute the values of x = -2, x = -3, x = -4 and x = -5 into the function:

`\begin{aligned}x=-2 \implies y&=(-2)/(-2+1)+3\\&=2+3\\&=5\end{aligned}`

`\begin{aligned}x=-3 \implies y&=(-2)/(-3+1)+3\\&=1+3\\&=4\end{aligned}`

`\begin{aligned}x=-4 \implies y&=(-2)/(-4+1)+3\\&=0.666...+3\\&=3.666...\end{aligned}`

`\begin{aligned}x=-5 \implies y&=(-2)/(-5+1)+3\\&=0.5+3\\&=3.5\end{aligned}`

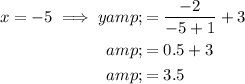
Plot the points (-2, 5), (-3, 4), (-4, 3.666...) and (-5, 3.5) on the given coordinate plane and draw a continuous curve through them.

End behaviour:

• As x approaches -1 from the negative side, x tends to ∞.
• As x approaches -∞, y approaches 3.