Question

the volume of a sphere is numerically equal to half its surface area. what is the radius of the sphere?

Answer 1

Hello !

Answer:

`\Large \boxed{\sf r=(3)/(2) }`

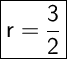
Explanation:

Let's remember :

• The volume of a sphere is given by
  `\sf V_(sphere)=(4)/(3) \pi r^3` where r is the radius.
• The surface area of a sphere is given by
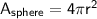  `\sf A_(sphere)=4\pi r^2` where r is the radius.

We know that the volume of the sphere is equal to half its surface area.

`\sf V_(sphere)=(1)/(2) A_(sphere)\\\\\sf (4)/(3)\pi r^3=(1)/(2) 4\pi r^2\\\\\sf (4)/(3)\pi r^3=2\pi r^2`

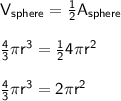
Let's solve this equation for r.

First, substract
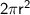`\sf 2\pi r^2` from both sides :

`\sf (4)/(3) \pi r^3-2\pi r^2=0`

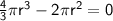
We can now factorize by taking out the highest common factor: 2r²

`\sf 2r^2((2)/(3) \pi r-\pi )=0`

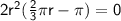
We can use the zero-product property.

There are two solutions :

• 
  `\sf 2r^2=0 \iff \boxed{\sf r=0}`
• 
  `\sf (2)/(3) \pi r -\pi =0 \iff \sf (2)/(3) \pi r =\pi \iff\boxed{ \sf r=(3)/(2) }`

The first solution is absurd : The radius of a sphere cannot be 0.

We conclude that we must keep the second solution.

Have a nice day ;)