Question

In a class of 42 students, the number of boys is 2/5 of the girls. Find the number of boys and girls in the class.

Answer 1

`\Huge \boxed{\bold{\text{12 Boys}}}`

`\Huge \boxed{\bold{\text{30 Girls}}}`

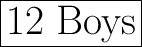
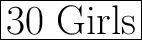
Explanation:

Let the number of girls be
`g` and the number of boys be
`b`.

According to the problem:
`b = (2)/(5) * g`

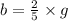
We also know that the total number of students is 42, so
`b + g = 42`.

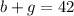Now, we have two equations with two variables:

1. 
   `b = (2)/(5) * g`
2. 
   `b + g = 42`

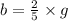
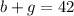
We can solve these equations to find the values of
`b` and
`g`.

Step 1: Solve for
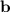`\bold{b}` in terms of
`\bold{g}`

From the first equation, we have
`b = (2)/(5) * g`

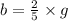
Step 2: Substitute the expression for
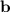`\bold{b}` into the second equation

Replace
`b` in the second equation with the expression we found in step 1.

`(2)/(5) * g + g = 42`

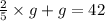
Step 3: Solve for
`\bold{g}`

Now, we have an equation with only one variable,
`g`:

`(2)/(5) * g + g = 42`

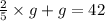
To solve for
`g`, first find a common denominator for the fractions:

`(2)/(5) * g + (5)/(5) * g = 42`

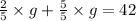
Combine the fractions:

`(7)/(5) * g = 42`

Now, multiply both sides of the equation by
`(5)/(7)` to isolate
`g`:

• 
  `g = 42 * (5)/(7)`
• 
  `g = 30`

Step 4: Find the value of
`\bold{b}`

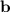
Now that we have the value of
`g`, we can find the value of
`b` using the first equation:

• 
  `b = (2)/(5) * g`
• 
  `b = (2)/(5) * 30`
• 
  `b = 12`

So, there are 12 boys and 30 girls in the class.

----------------------------------------------------------------------------------------------------------

Answer 2

BOYS = 30.

GIRLS = 12.

Explanation:

Boys: B

Girls: G

B = (2/5)G

B + G = 42.

(2/5)G + G = 42

2G + 5G = 210

7G = 210

G = 210/7

G = 30.

B = (2/5)G

B = (2/5)(30)

B = 60/5

B = 12.