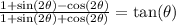Question

Help me to solve this ​

Answer 1

To prove the equation

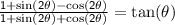`\sf\:(1 + \sin(2\theta) - \cos(2\theta))/(1 + \sin(2\theta) + \cos(2\theta)) = \tan(\theta)\\`, we will simplify the left-hand side and show that it is equal to the right-hand side.

Starting with the left-hand side:

`\sf\:(1 + \sin(2\theta) - \cos(2\theta))/(1 + \sin(2\theta) + \cos(2\theta)) \\`

Let's manipulate the numerator first. Using the double-angle identities, we have:

`\sf\:\sin(2\theta) = 2\sin(\theta)\cos(\theta) \\`

`\sf\:\cos(2\theta) = \cos^2(\theta) - \sin^2(\theta) = 1 - 2\sin^2(\theta) \\`

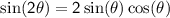
Substituting these expressions into the numerator:

`\sf\:1 + \sin(2\theta) - \cos(2\theta) = 1 + 2\sin(\theta)\cos(\theta) - (1 - 2\sin^2(\theta)) \\`

Simplifying the numerator:

`\sf\:1 + 2\sin(\theta)\cos(\theta) - 1 + 2\sin^2(\theta) = 2\sin(\theta)\cos(\theta) + 2\sin^2(\theta) \\`

Factoring out a common factor of 2:

`\sf\:2(\sin(\theta)\cos(\theta) + \sin^2(\theta)) \\`

Using the identity
`\sf\:\sin^2(\theta) = 1 - \cos^2(\theta)`, we can rewrite the numerator as:

`\sf\:2(\sin(\theta)\cos(\theta) + (1 - \cos^2(\theta))) \\`

Simplifying further:

`\sf\:2(\sin(\theta)\cos(\theta) + 1 - \cos^2(\theta)) \\`

Now, let's simplify the denominator:

`\sf\:1 + \sin(2\theta) + \cos(2\theta) = 1 + 2\sin(\theta)\cos(\theta) + (1 - 2\sin^2(\theta)) \\`

Simplifying the denominator:

`\sf\:1 + 2\sin(\theta)\cos(\theta) + 1 - 2\sin^2(\theta) = 2\sin(\theta)\cos(\theta) + 2(1 - \sin^2(\theta)) \\`

Using the identity
`\sf\:\sin^2(\theta) = 1 - \cos^2(\theta)`, we can rewrite the denominator as:

`\sf\:2\sin(\theta)\cos(\theta) + 2(1 - \cos^2(\theta))\\`

Simplifying further:

`\sf\:2\sin(\theta)\cos(\theta) + 2 - 2\cos^2(\theta) \\`

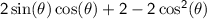
Now, we can substitute the simplified numerator and denominator back into the original equation:

`\sf\:(2(\sin(\theta)\cos(\theta) + 1 - \cos^2(\theta)))/(2\sin(\theta)\cos(\theta) + 2 - 2\cos^2(\theta))\\`

Canceling out the common factors of 2 in the numerator and denominator:

`\sf\:(\sin(\theta)\cos(\theta) + 1 - \cos^2(\theta))/(\sin(\theta)\cos(\theta) + 1 - \cos^2(\theta))\\`

Simplifying further, we can see that the numerator and denominator are equal:

`1`

Therefore, we have shown that:

`\sf\:(1 + \sin(2\theta) - \cos(2\theta))/(1 + \sin(2\theta) + \cos(2\theta)) = 1\\`

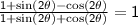
And since
`\sf\:1 = \tan(\theta)`, we have proven the original equation:

`(1 + \sin(2\theta) - \cos(2\theta))/(1 + \sin(2\theta) + \cos(2\theta)) = \tan(\theta)\\`