Question

Consider the equation x^3 - 3x^2 + 2x - 6 = 0. Find all the complex roots of this equation and represent them in the form a + bi.

Answer 1

x=i
`√(2)`, x=-i
`√(2)`

Explanation:

This equation can be factored. In order to do so, we can split the expression into two parts: (x^3-3x^2) and (2x-6). The greatest common factor of the first group is x^2, factoring it out gives us x^2(x-3). The greatest common factor of the second group is 2, factoring it out gives us 2(x-3). Since both x^2 and 2 are being multiplied by x-3, we add them into a factored form of (x^2+2)(x-3)=0

x-3 provides us with one real root, so we can disregard it.
x^2+2=0 ---> x^2=-2--->x=±
`√(-2)`
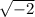
Factoring out the imaginary number i (equals
`√(-1)`), we get x=±i
`√(2)`