Question

Non Shaded Shaded
Area
Area
8
Find the radius
of the small circle

Answer 1

The answer is 16pi or 50.3cm² to 1 d.p

Explanation:

The non shaded=area of shaded

d=8

r=d/2=4

A=pir³

A=p1×4²

A=pi×16

A=16picm² or 50.3cm² to 1d.p

Answer 2

3.45 cm (3 s.f.)

Explanation:

We have been given a 5-sided regular polygon inside a circumcircle. A circumcircle is a circle that passes through all the vertices of a given polygon. Therefore, the radius of the circumcircle is also the radius of the polygon.

To find the radius of a regular polygon given its side length, we can use this formula:

`\boxed{\begin{minipage}{6 cm}\underline{Radius of a regular polygon}\\\\$r=(s)/(2\sin\left((180^(\circ))/(n)\right))$\\\\\\where:\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}`

Substitute the given side length, s = 8 cm, and the number of sides of the polygon, n = 5, into the radius formula to find an expression for the radius of the polygon (and circumcircle):

`\begin{aligned}\implies r&=(8)/(2\sin\left((180^(\circ))/(5)\right))\\\\ &=(4)/(\sin\left(36^(\circ)\right))\\\\ \end{aligned}`

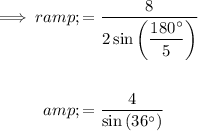
The formulas for the area of a regular polygon and the area of a circle given their radii are:

`\boxed{\begin{minipage}{6 cm}\underline{Area of a regular polygon}\\\\$A=(nr^2\sin\left((360^(\circ))/(n)\right))/(2)$\\\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}`

`\boxed{\begin{minipage}{6 cm}\underline{Area of a circle}\\\\$A=\pi r^2$\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

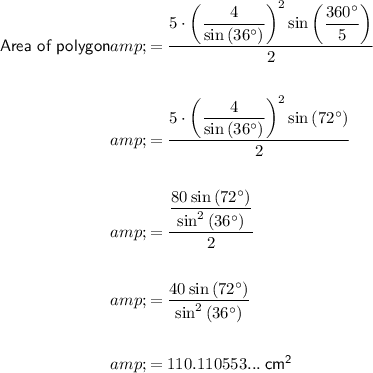
Therefore, the area of the regular pentagon is:

`\begin{aligned}\textsf{Area of polygon}&=(5 \cdot \left((4)/(\sin\left(36^(\circ)\right))\right)^2\sin\left((360^(\circ))/(5)\right))/(2)\\\\&=(5 \cdot \left((4)/(\sin\left(36^(\circ)\right))\right)^2\sin\left(72^(\circ)\right))/(2)\\\\&=((80\sin\left(72^(\circ)\right))/(\sin^2\left(36^(\circ)\right)))/(2)\\\\&=(40\sin\left(72^(\circ)\right))/(\sin^2\left(36^(\circ)\right))\\\\&=110.110553...\; \sf cm^2\end{aligned}`

The area of the circumcircle is:

`\begin{aligned}\textsf{Area of circumcircle}&=\pi \left((4)/(\sin\left(36^(\circ)\right))\right)^2\\\\&=(16\pi)/(\sin^2\left(36^(\circ)\right))\\\\&=145.489779...\; \sf cm^2\end{aligned}`

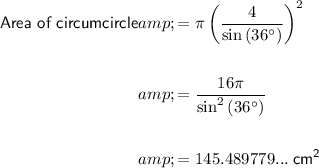
The area of the shaded area is the area of the circumcircle less the area of the regular pentagon plus the area of the small central circle.

The area of the unshaded area is the area of the regular pentagon less the area of the small central circle.

Given the shaded area is equal to the unshaded area:

`\begin{aligned}\textsf{Shaded area}&=\textsf{Unshaded area}\\\\\sf Area_(circumcircle)-Area_(polygon)+Area_(circle)&=\sf Area_(polygon)-Area_(circle)\\\\\sf 2\cdot Area_(circle)&=\sf 2\cdot Area_(polygon)-Area_(circumcircle)\\\\2\pi r^2&=2 \cdot (40\sin\left(72^(\circ)\right))/(\sin^2\left(36^(\circ)\right))-(16\pi)/(\sin^2\left(36^(\circ)\right))\\\\2\pi r^2&=(80\sin\left(72^(\circ)\right))/(\sin^2\left(36^(\circ)\right))-(16\pi)/(\sin^2\left(36^(\circ)\right))\\\\\end{aligned}`

`\begin{aligned}2\pi r^2&=(80\sin\left(72^(\circ)\right)-16\pi)/(\sin^2\left(36^(\circ)\right))\\\\r^2&=(40\sin\left(72^(\circ)\right)-8\pi)/(\pi \sin^2\left(36^(\circ)\right))\\\\r&=\sqrt{(40\sin\left(72^(\circ)\right)-8\pi)/(\pi \sin^2\left(36^(\circ)\right))}\\\\r&=3.44874763...\sf cm\end{aligned}`

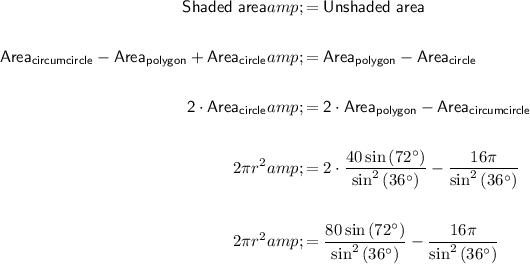
Therefore, the radius of the small circle is 3.45 cm (3 s.f.).