Question

Trina has a credit card that uses the adjusted balance method. For the first 10

days of one of her 30-day billing cycles, her balance was $780. She then
made a purchase for $170, so her balance jumped to $950, and it remained
that amount for the next 10 days. Trina then made a payment of $210, so her
balance for the last 10 days of the billing cycle was $740. If her credit card's
APR is 17%, which of these expressions could be used to calculate the
amount Trina was charged in interest for the billing cycle?
OA. (30)($780)
365
B.
O C.
D.
0.17
365
0.17
365
0.17
365
30
30
(10 $780+10 $950 +10 $210)
30
10
$780+10$950+10 $740
30
•30) ($570)

Answer 1

To calculate the amount Trina was charged in interest for the billing cycle using the adjusted balance method, the expression (10 * $780 + 10 * $950 + 10 * $740) / 30 * (0.17 / 365) can be used.

Step-by-step explanation:

To calculate the amount Trina was charged in interest for the billing cycle, we need to use the adjusted balance method.

This method calculates interest based on the average daily balance for the entire billing cycle. We can calculate the average daily balance by summing up the balances for each day and dividing it by the number of days in the billing cycle.

In this case, Trina had a balance of $780 for the first 10 days, a balance of $950 for the next 10 days, and a balance of $740 for the last 10 days.

The expression that can be used to calculate the amount of interest charged for the billing cycle is:

(10 * $780 + 10 * $950 + 10 * $740) / 30 * (0.17 / 365)

Answer 2

The correct expression for calculating the interest charged is B) ( (0.17)/365 · 30)( (10· $780+10· $950+10· $740)/30 )

To calculate the interest charged using the adjusted balance method, we need to consider the average daily balance over the billing cycle. The formula for interest charged is given by:

`\[ \text{Interest} = \frac{\text{APR}}{365} * \text{Number of Days in Billing Cycle} * \text{Average Daily Balance} \]`

Now, let's calculate the average daily balance for each scenario:

1. For the first 10 days: $780

2. After the purchase, for the next 10 days: $950

3. After the payment, for the last 10 days: $740

The average daily balance
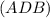`(\(ADB\))` is the sum of the daily balances divided by the number of days:

`\[ ADB = ((10 * 780 + 10 * 950 + 10 * 740))/(30) \]`

Now, substitute the values into the interest formula:

`\[ \text{Interest} = (0.17)/(365) * 30 * ADB \]`

Comparing this with the given options:

`\[ \text{Option B: } \left( (0.17)/(365) * 30 \right) \left( (10 * 780 + 10 * 950 + 10 * 740)/(30) \right) \]`

Therefore, the correct expression to calculate the interest charged for the billing cycle is Option B.

The question probable maybe:

Trina has a credit card that uses the adjusted balance method. For the first 10 days of one of her 30-day billing cycles, her balance was $780. She then made a purchase for $170, so her balance jumped to $950, and it remained that amount for the next 10 days. Trina then made a payment of $210, so her balance for the last 10 days of the billing cycle was $740. If her credit card's APR is 17%, which of these expressions could be used to calculate the amount Trina was charged in interest for the billing cycle?

A. ( (0.17)/365 · 30)($570)

B. ( (0.17)/365 · 30)( (10· $780+10· $950+10· $740)/30 )

C. ( (0.17)/365 · 30)( (10· $780+10· $950+10· $210)/30 )

D. ( (0.17)/365 · 30)($780)