Question

Particles q₁ = +18.1 µC, q2 = -11.2 μC, and 93 = +5.67 μC are in a line. Particles q₁ and q2 are separated by 0.280 m and particles q2 and q3 are separated by 0.350 m. What is the net force on particle q₂? ​

Answer 1

`\vec F_(net \ on \ q_2)=15.9637N}} \ \text{at 180\textdegree (or to the left/negative x-axis)}`

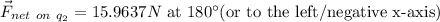
Step-by-step explanation:

Using Coulomb's law to answer this question.

`\boxed{\left\begin{array}{ccc}\text{\underline{Coloumb's Law:}}\\\\\vec F_e=(k_eq_1q_2)/(r^2) \cdot \hat r \end{array}\right}`

• 
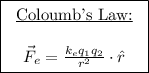
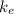  `k_e` is Coulomb's constant (
  `8.99 *10^9(Nm^2)/(C^2)`)
• 
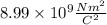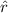  `\hat r` is a direction vector that points towards the charge you are calculating the force on

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Given:

`q_1=18.1 \ \mu C \rightarrow 18.1 * 10 ^(-6) \ C\\r_{2_(1)}=0.280 \ m\\q_2=-11.2 \ \mu C \rightarrow -11.2 * 10 ^(-6) \ C\\q_3=5.67 \ \mu C \rightarrow 5.67 * 10 ^(-6)\ C\\r_{2_(3)}=0.350 \ m`

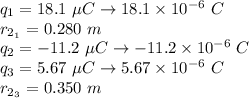
Find:

`|| \vec F_{net \ on \ q_(2)}||= \ ?? \ N`

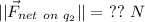
**Assuming q_2 is the center of a coordinate system.

(1) - Find the force on q_2 exerted by q_1

`\vec F_{2_(1)}=\frac{k_eq_2q_1}{(r_{2_(1)})^2} \cdot \hat r_{2_(1)}\\\\\Longrightarrow \vec F_{2_(1)}=((8.99 * 10^(9))(-11.2 * 10^(-6))(18.1 * 10^(-6)))/((0.280)^2) \cdot ( < 0.280,0 > )/(√((0.280)^2+(0)^2) ) \\\\\Longrightarrow \vec F_{2_(1)}=-23.2456 \cdot < 1,0 > \\\\\therefore \boxed{\vec F_{2_(1)}= < -23.2456,0 > N}`

(2) - Find the force on q_2 exerted by q_3

`\vec F_{2_(1)}=\frac{k_eq_2q_3}{(r_{2_(3)})^2} \cdot \hat r_{2_(3)}\\\\\Longrightarrow \vec F_{2_(3)}=((8.99 * 10^(9))(-11.2 * 10^(-6))(5.67 * 10^(-6)))/((0.280)^2) \cdot ( < - 0.350,0 > )/(√((-0.350)^2+(0)^2) ) \\\\\Longrightarrow \vec F_{2_(3)}=-7.2819 \cdot < -1,0 > \\\\\therefore \boxed{\vec F_{2_(3)}= < 7.2819,0 > N}`

(3) - Find the net charge on q_2

`\vec F_(net \ on \ q_2)=\vec F_{2_(1)}+\vec F_{2_(3)}\\\\\text{Recall that} \ \vec F_{2_(1)}= < -23.2456,0 > N \ \text{and} \ \vec F_{2_(3)}= < 7.2819,0 > N\\\\\Longrightarrow \vec F_(net \ on \ q_2)= < -23.2456,0 > + < 7.2819,0 > \\\\\therefore \boxed{\vec F_(net \ on \ q_2)= < -15.9637,0 > N}\\\\\Longrightarrow ||\vec F_(net \ on \ q_2)||=√((-15.9637)^2+(0)^2) \\\\\therefore \boxed{\boxed=15.9637N} \ \text{at 180\textdegree (or to the left/negative x-axis)}`