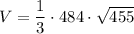Question

What is the volume of the pyramid

Answer 1

`V = (484)/(3) √(455)`

Explanation:

The formula for the volume of a square pyramid is:

`V = (1)/(3)bh`

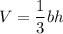
where
`b` is the area of the pyramid's base, and
`h` is its vertical height.

In the diagram for this problem, we are given the slant height, not the vertical height which is needed to find the volume of the pyramid.

So, we can solve for the vertical height by applying the Pythagorean Theorem to a partial cross-section.

`a^2 + b^2 = c^2`

`(22/2)^2 + h^2 = 24^2`

`121 + h^2 = 576`

`h^2 = 455`

`h = √(455)`

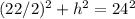
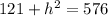
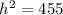
Now, we can plug the pyramid's dimensions into the above formula and solve for its volume. Remember that the area of a square is:
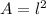`A = l^2` where
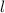`l` is the square's side length.

`V = (1)/(3) (22^2) \cdot \sqrt{455`

`V = (1)/(3) \cdot 484 \cdot \sqrt{455`

`\boxed{V = (484)/(3) √(455)}`