Question

Can someone please help me with these geometry question??!! Worth Points!!

Answer 1

x = 16 , MJ ≈ 8.1

Explanation:

5

the inscribed angle JKL is half the measure of the arc JL that subtends it, so

9x = 2 × 72 = 144 ( divide both sides by 9 )

x = 16

6

the angle between tangent KJ and diameter JL at the point of contact is right, that is ∠ KJL = 90°

then Δ KJL is a right triangle

using Pythagoras' identity in the right triangle

KJ² + JL² = KL²

10² + JL² = 19²

100 + JL² = 361 ( subtract 100 from both sides )

JL² = 261 ( take square root of both sides )

JL =
`√(261)`

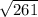
MJ is the radius of the circle and is half the diameter JL

MJ =
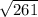`√(261)` ÷ 2 ≈ 8.1 ( to 1 decimal place )