Question

"Consider the following circle with radius 1. The lines A and B are radii, and have a length of 1. Find the area of the shaded region."

I got an area of 1.06 (Rounded), I'm just wondering if that is correct. Any help would be appreciated!

Answer 1

`\textsf{Area}=(5\pi -3)/(12) \approx 1.06\; \sf square\;units \;(3\;s.f.)\end{aligned}`

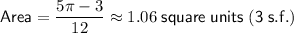
Explanation:

To find the area of the shaded region, subtract the area of the isosceles triangle from the area of the sector.

An isosceles triangle is made up of two congruent right triangles.

To find the height of the right triangles (and thus the height of the isosceles triangle), use the cosine trigonometric ratio.

`\boxed{\begin{minipage}{9 cm}\underline{Cosine trigonometric ratio} \\\\$\sf \cos(\theta)=(A)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Given values:

• The angle is half the apex angle: θ = 5π/12.
• The side adjacent the angle is the height of the triangle: x.
• The hypotenuse is the radius: H = 1.

Substitute these values into the cosine ratio to calculate the height of the right triangles (and thus the height of the isosceles triangle):

`\cos \left((5\pi)/(12)\right)=(x)/(1)`

`x=\cos \left((5\pi)/(12)\right)`

`x=(√(6)-√(2))/(4)`

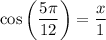
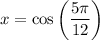
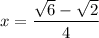
The base of one of the right triangles can be found by using the sine trigonometric ratio.

`\boxed{\begin{minipage}{9 cm}\underline{Sine trigonometric ratio} \\\\$\sf \sin(\theta)=(O)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Given values:

• The angle is half the apex angle: θ = 5π/12.
• The side opposite the angle is the base of the right triangle: y.
• The hypotenuse is the radius: H = 1.

Substitute these values into the sine ratio to determine the base of the right triangle:

`\sin \left((5\pi)/(12)\right)=(y)/(1)`

`y=\sin \left((5\pi)/(12)\right)`

`y=(√(6)+√(2))/(4)`

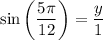
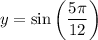
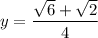
The base of the isosceles triangle is twice the base of the right triangle, so the base of the isosceles triangle = 2y.

Therefore the area of the isosceles triangle is:

`\begin{aligned}\textsf{Area of isosceles triangle}&=(1)/(2) \cdot \sf base \cdot height\\\\&=(1)/(2)\cdot 2y \cdot x\\\\&=(1)/(2) \cdot 2\left((√(6)+√(2))/(4)\right) \cdot \left((√(6)-√(2))/(4)\right)\\\\&=\left((√(6)+√(2))/(4)\right) \cdot \left((√(6)-√(2))/(4)\right)\\\\&=(4)/(16)\\\\&=(1)/(4)\sf \;square\;units\end{aligned}`

To find the area of the sector of the circle, use the area of a sector formula (where the angle is measured in radians).

`\boxed{\begin{minipage}{6.4 cm}\underline{Area of a sector}\\\\$A=\frac12 r^2 \theta$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in radians.\\\end{minipage}}`

Given values:

• r = 1

• θ = 5π/6

Substitute the values into the formula:

`\begin{aligned}\textsf{Area of the sector}&=(1)/(2) \cdot (1)^2 \cdot (5\pi)/(6)\\\\&=(1)/(2) \cdot 1 \cdot (5\pi)/(6)\\\\&=(1)/(2) \cdot (5\pi)/(6)\\\\&=(5\pi)/(12)\;\; \sf square\;units\end{aligned}`

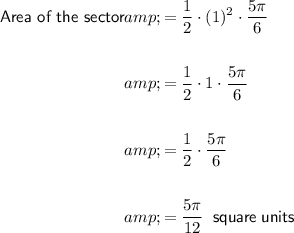
Finally, to find the area of the shaded region, subtract the area of the isosceles triangle from the area of the sector:

`\begin{aligned}\textsf{Area of the shaded region}&=\sf Area_(sector)-Area_(isosceles\;triangle)\\\\&=(5\pi)/(12)-(1)/(4)\\\\&=(5\pi)/(12)-(3)/(12)\\\\&=(5\pi -3)/(12)\\\\&=1.05899693...\\\\&=1.06\; \sf square\;units \;(3\;s.f.)\end{aligned}`

Therefore, the area of the shaded region is (5π - 3)/12 or approximately 1.06 square units (3 significant figures).