Question

(q66) Approximate the integral
using Trapezoidal rule, where n = 4.

Answer 1

A. 1.921

Explanation:

The Trapezoid Rule is a numerical method used to approximate the value of a definite integral. It is based on approximating the area under a curve by dividing it into a series of trapezoids and summing their areas.

The general formula for the Trapezoid Rule is as follows:

`\displaystyle \int_(a)^(b) y\: \:\text{d}x \approx (1)/(2)h\left[(y_0+y_n)+2(y_1+y_2+...+y_(n-1))\right] \quad \textsf{where }h=(b-a)/(n)`

Essentially, this means add the first and last heights (y₀ + yₙ) to twice the sum of all the other heights, then multiply the result by h/2.

Given definite integral:

`\displaystyle \int^3_1 \left(\sin√(x)\right)\; \text{d}x`

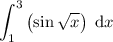
Therefore:

• 
  `y = \sin √(x)`
• a = 1
• b = 3

Given n = 4, calculate the value of h (the width of each trapezoid):

`h=(3-1)/(4)=(2)/(4)=(1)/(2)`

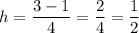
Therefore, the width of each trapezoid is 0.5.

This gives the values of x₀ = 1, x₁ = 1.5, x₂ = 2, x₃ = 2.5, and x₄ = 3.

Calculate the value of y for each of value of x:

`\begin{array}c\cline{1-6}\vphantom{\frac12}x&1&1.5&2&2.5&3\\\cline{1-6}\vphantom{\frac12}y&\sin √(1)&\sin √(1.5)&\sin √(2)&\sin √(2.5)&\sin √(3)\\\cline{1-6}\end{array}`

Now use the formula to find the approximate value of the integral:

`\begin{aligned}\displaystyle \int_(1)^(3) \left(\sin √(x)\right)\: \:\text{d}x & \approx (1)/(2)\cdot (1)/(2)\left[(\sin√(1)+\sin √(3))+2(\sin √(1.5)+\sin √(2)+\sin √(2.5))\right]\\\\&=(1)/(4)\left[1.828...+2(2.928...)\right]\\\\&=(1)/(4)\left[1.828...+5.856...\right]\\\\&=(1)/(4)\left[7.685...\right]\\\\&=1.92134030...\\\\&=1.921\; \sf (3\;d.p.)\end{aligned}`

Therefore the approximation of the integral using the Trapezoid Rule is 1.921.