Question

A spring is laid sideways on an air hockey table. It has a spring constant of 26.0 N/m. If a 2.45 kg air-hockey puck traveling at 1.50 m/s bounces into the spring, how much will the spring

compress before the puck is brought to rest?
(Hint: you will need to calculate how much WORK is done to slow the puck. Consult your notes and remember that work is a change in kinetic energy: KE)

__cm?

Answer 1

Answer: 46.0455 cm

Step-by-step explanation:

The kinetic energy of the puck is 2.75625 Joules.

This energy is used to compress the spring and bring the puck to rest. The work done on the puck by the spring is equal to the change in kinetic energy of the puck, which is the kinetic energy it initially had.

The work done on the puck by the spring can also be expressed as the potential energy stored in the spring at the point of maximum compression, which is given by the formula
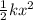`\( (1)/(2) k x^2 \)`, where
`\( k \)` is the spring constant and
`\( x \)` is the distance the spring is compressed.

Setting these two expressions for the work done equal to each other gives:

`\( (1)/(2) k x^2 = 2.75625 J \)`

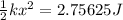
We can solve this equation for \( x \), the distance the spring is compressed.

The spring will compress approximately 0.460455 meters, or 46.0455 cm, before the puck is brought to rest.