Question

Solve the differential equation y

′′
+
2
y
′
+
y
=
e
−
2
t
ln
t
by variation of parameters.

Answer 1

`y(t)=c_1e^(-t)+c_2te^(-t)+(1)/(2)t^2\ln(t)e^(-t)-(3)/(4) t^2e^(-t)`

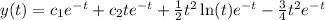
Explanation:

Given the second-order differential equation. Solve by using variation of parameters.

`y''+2y'+y=e^(-t)\ln(t)`

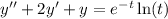
(1) - Solve the DE as if it were homogeneous to find the homogeneous solution

`y''+2y'+y=e^(-t)\ln(t) \Longrightarrow y''+2y'+y=0\\\\\text{The characteristic equation} \rightarrow m^2+2m+1=0, \ \text{solve for m}\\\\m^2+2m+1=0\\\\\Longrightarrow (m+1)(m+1)=0\\\\\therefore \boxed{m=-1,-1}`

`\boxed{\left\begin{array}{ccc}\text{\underline{Solutions to Higher-order DE's:}}\\\\\text{Real,distinct roots} \rightarrow y=c_1e^(m_1t)+c_2e^(m_2t)+...+c_ne^(m_nt)\\\\ \text{Duplicate roots} \rightarrow y=c_1e^(mt)+c_2te^(mt)+...+c_nt^ne^(mt)\\\\ \text{Complex roots} \rightarrow y=c_1e^(\alpha t)\cos(\beta t)+c_2e^(\alpha t)\sin(\beta t)+... \ ;m=\alpha \pm \beta i\end{array}\right}`

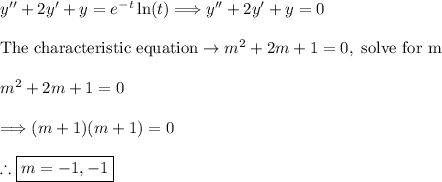
Notice we have repeated/duplicate roots, form the homogeneous solution.

`\boxed{\boxed{y_h=c_1e^(-t)+c_2te^(-t)}}`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

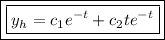
Now using the method of variation of parameters, please follow along very carefully.

`\boxed{\left\begin{array}{ccc}\text{\underline{Variation of Parameters Method(1 of 2):}}\\ \text{Given a DE in the form} \rightarrow ay''+by`

`\boxed{\left\begin{array}{ccc}\text{\underline{Variation of Parameters Method(2 of 2):}}\\ \text{3. Find} \ W_1, \ W_2, \dots, \ W_n.\\ \\ \text{4. Find} \ u_1, \ u_2, \dots, \ u_n. \\ \Rightarrow u_n= \int(W_n)/(|W|) \\ \\ \text{5. Form the particular solution.} \\ \Rightarrow y_p=u_1y_1+u_2y_2+ \dots+ u_ny_n \\ \\ \text{6. Form the general solution.}\\ y_(gen.)=y_h+y_p\end{array}\right}`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

(2) - Finding the Wronksian determinant

`|W|= \left|\begin{array}{ccc}e^(-t)&te^(-t)\\-e^(-t)&e^(-t)-te^(-t)\end{array}\right|\\\\\Longrightarrow (e^(-t))(e^(-t)-te^(-t))-(te^(-t))(-e^(-t))\\\\\Longrightarrow (e^(-2t)-te^(-2t))-(-te^(-2t))\\\\\therefore \boxed`

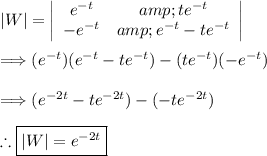
(3) - Finding W_1 and W_2

`W_1=\left|\begin{array}{ccc}0&y_2\\g(t)&y_2'\end{array}\right| \ \text{Recall:} \ g(t)=e^(-t) \ln(t)\\\\\Longrightarrow \left|\begin{array}{ccc}0&te^(-t)\\e^(-t) \ln(t)&e^(-t)-te^(-t)\end{array}\right|\\\\\Longrightarrow 0-(te^(-t))(e^(-t) \ln(t))\\\\\therefore \boxed{W_1=-t\ln(t)e^(-2t)}`

`W_2=\left|\begin{array}{ccc}y_1&0\\y_1'&g(t)\end{array}\right| \ \text{Recall:} \ g(t)=e^(-t) \ln(t)\\\\\Longrightarrow \left|\begin{array}{ccc}e^(-t)&0\\-e^(-t)&e^(-t) \ln(t)\end{array}\right|\\\\\Longrightarrow (e^(-t))(e^(-t) \ln(t))-0\\\\\therefore \boxed{W_2=\ln(t)e^(-2t)}`

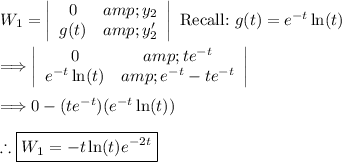
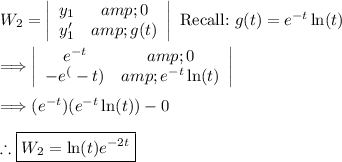
(4) - Finding u_1 and u_2

`u_1=\int (W_1)/(|W|); \text{Recall:} \ W_1=-t\ln(t)e^(-2t) \ \text{and} \ |W|=e^(-2t) \\\\\Longrightarrow \int(-t\ln(t)e^(-2t))/(e^(-2t)) dt\\\\\Longrightarrow -\int t\ln(t)dt \ \text{(Apply integration by parts)}\\\\\\\boxed{\left\begin{array}{ccc}\text{\underline{Integration by Parts:}}\\\\uv-\int vdu\end{array}\right }\\\\\text{Let} \ u=\ln(t) \rightarrow du=(1)/(t)dt \\\\\text{an let} \ dv=tdt \rightarrow v=(1)/(2)t^2 \\\\`

`\Longrightarrow -\Big[(\ln(t))((1)/(2)t^2)-\int [((1)/(2)t^2)((1)/(t)dt)]\Big]\\\\\Longrightarrow -\Big[(1)/(2)t^2\ln(t)-(1)/(2)\int (t)dt\Big]\\\\\Longrightarrow -\Big[(1)/(2)t^2\ln(t)-(1)/(2)\cdot(1)/(2)t^2 \Big]\\\\\therefore \boxed{u_1=(1)/(4)t^2-(1)/(2)t^2\ln(t)}`

`u_2=\int (W_2)/(|W|); \text{Recall:} \ W_2=\ln(t)e^(-2t) \ \text{and} \ |W|=e^(-2t) \\\\\Longrightarrow \int(\ln(t)e^(-2t))/(e^(-2t)) dt\\\\\Longrightarrow \int \ln(t)dt \ \text{(Once again, apply integration by parts)}\\\\\text{Let} \ u=\ln(t) \rightarrow du=(1)/(t)dt \\\\\text{an let} \ dv=1dt \rightarrow v=t \\\\\Longrightarrow (\ln(t))(t)-\int[(t)((1)/(t)dt )] \\\\\Longrightarrow t\ln(t)-\int 1dt\\\\\therefore \boxed{u_2=t \ln(t)-t}`

(5) - Form the particular solution

`y_p=u_1y_1+u_2y_2\\\\\Longrightarrow ((1)/(4)t^2-(1)/(2)t^2\ln(t))(e^(-t))+(t \ln(t)-t)(te^(-t))\\\\\Longrightarrow(1)/(4)t^2e^(-t)-(1)/(2)t^2\ln(t)e^(-t)+ t^2\ln(t)e^(-t)-t^2e^(-t)\\\\\therefore \boxed{ y_p=(1)/(2)t^2\ln(t)e^(-t)-(3)/(4) t^2e^(-t)}`

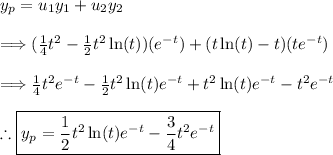
(6) - Form the solution

`y_(gen.)=y_h+y_p\\\\\therefore\boxed{\boxed{y(t)=c_1e^(-t)+c_2te^(-t)+(1)/(2)t^2\ln(t)e^(-t)-(3)/(4) t^2e^(-t)}}`

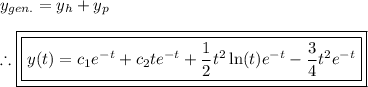
Thus, the given DE is solved.