Question

HELP FIND SURFACE AREA OF PYRAMID

Answer 1

Figure 1: 623.2 in²

Figure 2: 679.8 in²

Explanation:

For a pyramid total surface area

= Base Area + Lateral Surface Area

Figure 1 is a triangular prism
It's base is an equilateral triangle with side = 20 in
Area of an equilateral triangle =
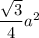`(√(3))/(4) a^2` where
`a` is the length of the base

So in figure 1, base area = area of equilateral triangle with side a = 20 in

`\text{Base Area =} (√(3))/(4) \cdot 20^2 \approx 173.2 \;in^2`

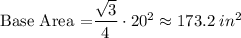
Each lateral side is an isosceles triangle with base = 20 and height = 15
Area of each triangle

`= (1)/(2) \cdot base \cdot height`

`= (1)/(2) \cdot 20 \cdot 15 \\\\= 150 \; in^2`

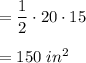
There are three such lateral sides so total lateral area = 150 x 3 = 450 in²

Total surface area = 173.21 + 450 = 623.2 in²

Figure 2
This is a regular hexagonal pyramid

The base is a regular hexagon of side 10

Base area = Area of hexagon of side 10

Area of a regular hexagon with side a

`= (3√(3))/(4) a^2`

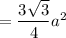
Base area of Figure 2

`= (3√(3))/(4) 10^2\\\\\approx 259.8 \;in^2`

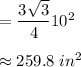
The lateral surface consists of 6 isosceles triangles each with a base = 10 in and height = 14 in

Area of each isosceles triangle

`= (1)/(2) \cdot 10 \cdot 14 \\\\= 70 \;in^2`

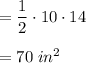
Since there are 6 such lateral triangles, total lateral surface area
= 70 x 6 = 420 in²

So total surface area = base area + total lateral surface area
= 259.8 + 420 = 679.8 in²