Question

Which one of these answers is correct (show work please)

ignore the ones that start with i,ii, iii
100 POINTS!!!

Answer 1

`\textsf{5.} \quad \textsf{C)} \;\; \displaystyle \int^(13)_1 \sqrt{1+\left((1)/(4)\right)^2}\; \text{d}y`

`\textsf{6.} \quad \textsf{D)} \quad -(1)/(4)y^(-4)=(1)/(3)x^3-(1)/(4)`

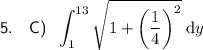
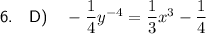
Explanation:

Question 5

To find the arc length of a given function between two points, we can use the Arc Length Formula:

`\boxed{\begin{minipage}{7.4cm}\underline{Arc Length Formula}\\\\$\displaystyle \int_(a)^(b) √(1+(f'(x))^2)\; \text{d}x$\\\\\\where: \\ \phantom{ww}$\bullet$ $a$ and $b$ are the limits. \\ \phantom{ww}$\bullet$ $f'(x)$ is the first derivative of $f(x)$.\\\end{minipage}}`

The given function is:

`y=4x-3`

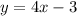
Differentiate the given function:

`\begin{aligned} f(x)&=4x-3\\ \implies f'(x)&=4\end{aligned}`

As the function is in terms of x, the interval [a, b] is the x-values of the given points. Therefore:

• 
  `a = 1`
• 
  `b = 4`

Set up the integral using the arc length formula:

`\displaystyle \textsf{Arc length}=\int^4_1 √(1+(4)^2)\; \text{d}x`

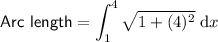
You will notice that this integral is not one of the given answer options.

We can also set up the integral with respect to y.

To do this, begin by rearranging the function so that x is a function of y:

`\begin{aligned}y&=4x-3\\y+3&=4x\\x&=(1)/(4)y+(3)/(4)\end{aligned}`

Differentiate x with respect to y:

`\begin{aligned} g(y)&=(1)/(4)y+(3)/(4)\\ \implies g'(y)&=(1)/(4)\end{aligned}`

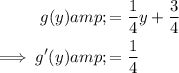
As the function is in terms of y, the interval [a, b] is the y-values of the given points. Therefore:

• 
  `a = 1`
• 
  `b = 13`

Set up the integral using the arc length formula:

`\boxed{\displaystyle \textsf{Arc length}=\int^(13)_1 \sqrt{1+\left((1)/(4)\right)^2}\; \text{d}y}`

Therefore, the correct answer option is option C.

`\hrulefill`

Question 6

The given differential equation is:

`\frac{\text{d}y}{\text{d}x}=x^2 \cdot y^5`

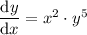
Solving a differential equation means using it to find an equation in terms of the two variables, without a derivative term.

Rearrange the equation so that all the terms containing y are on the left-hand side, and all the terms containing x are on the right-hand side:

`(1)/(y^5)\; \text{d}y=x^2 \; \text{d}x`

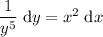
Integrate both sides:

`\displaystyle \int (1)/(y^5)\; \text{d}y=\int x^2 \; \text{d}x`

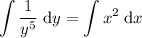
Use the following integration rule:

`\boxed{\begin{minipage}{4 cm}\underline{Integrating $x^n$}\\\\$\displaystyle \int x^n\:\text{d}x=(x^(n+1))/(n+1)+\text{C}$\end{minipage}}`

Therefore:

`\begin{aligned}\displaystyle \int (1)/(y^5)\; \text{d}y&=\int x^2 \; \text{d}x\\\\ \int y^(-5)\; \text{d}y&=\int x^2 \; \text{d}x\\\\(y^(-5+1))/(-5+1)&=(x^(2+1))/(2+1)+\text{C}\\\\(y^(-4))/(-4)&=(x^3)/(3)+\text{C}\\\\-(1)/(4)y^(-4)&=(1)/(3)x^3+\text{C}\end{aligned}`

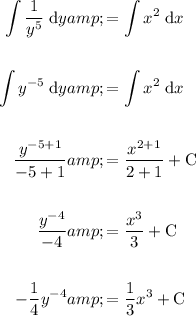
Given y(0) = 1, substitute y = 1 and x = 0 into the equation and solve for C:

`\begin{aligned}-(1)/(4)(1)^(-4)&=(1)/(3)(0)^3+\text{C}\\\\-(1)/(4)&=0+\text{C}\\\\\text{C}&=-(1)/(4)\end{aligned}`

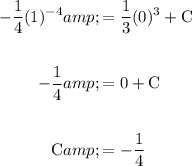
Therefore, the equation is:

`\boxed{-(1)/(4)y^(-4)=(1)/(3)x^3-(1)/(4)}`

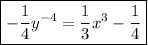
Therefore, the correct answer option is option D.

Answer 2

(5) - Option C,
`s=3√(17)`

(6) - Option D,
`-(1)/(4) y^(-4)=(1)/(3) x^3 -(1)/(4)`

Explanation:

Given the following questions.

(5) - Find the arc length of y=4x-3 from A(1,1) to B(4,13)

(6) - Solve the first-order differential equation
`y'=x^2y^5` with the initial condition,
`y(0)=1`.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Question #5:

`\boxed{\left\begin{array}{ccc}\text{\underline{Formula for Arc Length:}}\\\\s=\int\limits^b_a {√(1+(f'(x))^2) } \, dx \end{array}\right}`

(1) - Take the derivative of the function y

`y=4x-3\\\\\Longrightarrow \boxed{y'=4}`

(2) - Square y'

`y'=4\\\\\Longrightarrow y'=4^2\\\\\Longrightarrow \boxed{y'=16}`

(3) - Plug into the formula for arc length

`s=\int\limits^b_a {√(1+(f'(x))^2) } \, dx \\\\\text{Limits:} \ 1\leq x\leq 4\\\\\Longrightarrow\int\limits^4_1 {√(1+16) } \, dx \\\\\Longrightarrow\boxed{ \int\limits^4_1 {√(17) } \, dx} \\`

(4) - Solve the integral

`\int\limits^4_1 {√(17) } \, dx \\\\\Longrightarrow \Big [x√(17) \Big] \right]_(1)^(4)\\\\\Longrightarrow 4√(17) -√(17\\)\\\\ \therefore \boxed{s=3√(17) }`

Thus, the arc length is found.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Quick note: The question solved for the arc length using a dy integral not a dx integral (which was really unnecessary), so let me clarify that issue.

(1) - Taking the function y, and solving it for x

`y=4x-3\\\\\Longrightarrow y+3=4x\\\\\Longrightarrow \boxed{x=(1)/(4)y+(3)/(4)}`

(2) - Repeating steps (1)-(4) from above

`x=(1)/(4)y+(3)/(4)\\\\\Longrightarrow \boxed{x'=(1)/(4)} \\\\\Longrightarrow (x')^2=((1)/(4))^2\\\\\Longrightarrow \boxed{(x')^2=(1)/(16)}\\\\s=\int\limits^b_a {√(1+(f'(x))^2) } \, dy\\\text{Limits:} \ 1\leq y\leq 13\\\\ \Longrightarrow\int\limits^(13)_1 {\sqrt{1+(1)/(16) } \, dy\\\\ \Longrightarrow\int\limits^(13)_1 {\sqrt{(17)/(16) } \, dy\\\\ \Longrightarrow\int\limits^(13)_1 {(√(17) )/(4) } \, dy\\\\`

`\Longrightarrow\Big[(√(17) )/(4) y \Big]^(13)_(1)\\\\\Longrightarrow (13√(17) )/(4) -(√(17) )/(4) \\\\\ \Longrightarrow \boxed{\boxed{s=3√(17) }}`

Thus, the correct setup according to your question is option C.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Question #6:

The given differential equation is separable.

`\boxed{\left\begin{array}{ccc}\text{\underline{Seperable Differential Equation:}}\\(dy)/(dx) =f(x)g(y)\\\\\rightarrow\int(dy)/(g(y))=\int f(x)dx \end{array}\right }`

(1) - Solve the separable DE

`(dy)/(dx) =x^2y^5\\\\\Longrightarrow (1)/(y^5) dy=x^2dx\\\\\Longrightarrow \int y^(-5)dy= \int x^2 dx\\\\\Longrightarrow \boxed{ -(1)/(4) y^(-4)=(1)/(3) x^3 +C}`

(2) - Use the given initial condition to find the arbitrary constant "C"

`\text{Recall} \rightarrow y(0)=1\\\\-(1)/(4) y^(-4)=(1)/(3) x^3 +C\\\\\Longrightarrow -(1)/(4) (1)^(-4)=(1)/(3) (0)^3 +C\\\\\Longrightarrow -(1)/(4) (1)=0 +C\\\\\therefore \boxed{C=-(1)/(4) }`

(3) - Form the final solution

`\boxed{\boxed{-(1)/(4) y^(-4)=(1)/(3) x^3 -(1)/(4) }}`

Thus, option D is correct.