Question

Look at the simultaneous equations below.

x - 6y = 10
3y^2 = 4x+7

a) show that 3y^2 -24y - 47 = 0
b) use part a) to solve the simultaneous equations. If any of your answers are decimals, give them to 1 d.p.

It’s asking for two possibilities of x and y - someone please help!

Answer 1

(x, y) = (0.2, -1.6) or (67.8, 9.6)

Explanation:

You want the solution to the system of equations ...

• x -6y = 10
• 3y² = 4x +7

using substitution for x.

a) Substitution

The first equation can be used to write an expression for x:

x = 6y +10 . . . . . . add 6y to both sides

This can be substituted for x in the second equation:

3y² = 4(6y +10) +7

3y² = 24y +40 +7

3y² -24y -47 = 0 . . . . . . . subtract (24y+47) to get standard form

b) Solution

We can use the quadratic formula to solve this equation:

`y=(-b\pm√(b^2-4ac))/(2a)=(-(-24)\pm√((-24)^2-4(3)(-47)))/(2\cdot3)\\\\y=(24\pm√(24^2+12\cdot47))/(6)\approx\{9.6,-1.6\}`

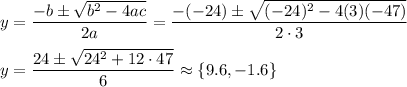
Then x can be found from the equation above as ...

x = 6y +10 = 34 ± √1140 ≈ {67.8, 0.2}

The solutions are (x, y) = (0.2, -1.6) or (67.8, 9.6).

<95141404393>