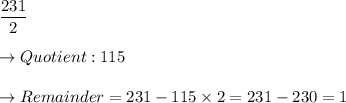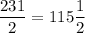Question

What is the volume of the prism?

Enter your answer, as a mixed number in simplest form, in the box.

Answer 1

`115 (1)/(2)\:cm^3`

Explanation:

The volume of a rectangular prism is the product of each of the sides of the prism

Given the sides have lengths

`3(1)/(2), 6 \;and\; 5 (1)/(2) cm`

the volume would be

`3(1)/(2) * 6 * 5 (1)/(2)`

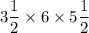
To perform this multiplication, convert mixed fractions to improper fractions first

Use the rule that mixed fraction

`a(b)/(c)=(a* \:c+b)/(c)`

`3(1)/(2)=(3* 2+1)/(2) = (7)/(2)`

`5(1)/(2)=(5* 2+1)/(2)= (11)/(2)`

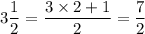
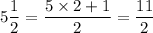
Therefore

`3(1)/(2)* \:6* \:5(1)/(2)\\\\= (7)/(2)* \:6* (11)/(2)\\\\= (7)/(2)* (6)/(1)* (11)/(2) \quad(6 = (6)/(1))`

`=(7* \:6* \:11)/(2* \:1* \:2)\\\\= (462)/(4)\\`

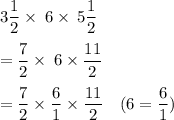
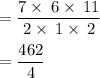
Divide numerator and denominator by 2 to get

`(231)/(2)\\`

Convert improper fraction
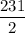`(231)/(2)` to mixed fraction using quotient/remainder

`(231)/(2) \\\\\rightarrow Quotient: 115\\\\\rightarrow Remainder = 231 - 115 * 2 = 231 - 230 = 1`

`(231)/(2) = 115 (1)/(2)`