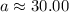Question

A girl views the angle of elevation of the top of a tower to be a°. She is 40m away from the foot of the tower and at the same level. If the height of the tower is 23.09m, find a​

Answer 1

`a \approx 30.00^`

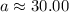
Explanation:

Main concepts:

Concept 1: Angle of elevation

Concept 2: Right Triangle trigonometry

Concept 1: Angle of elevation

An angle of elevation is the angle measured between two rays, starting from straight-ahead, to another ray pointing upward.

If she stands 40m from the base of the tower, and the tower is 23.09m tall, then the diagram can be drawn as attached.

Concept 2: Right Triangle trigonometry

The three basic trigonometric functions are Sine, Cosine, and Tangent. Each of these functions, when applied to an angle, gives the ratio of two sides of a right triangle that contains that angle:

`sin(\theta)=(opposite~side)/(hypotenuse)`

`cos(\theta)=(adjacent~side)/(hypotenuse)`

`tan(\theta)=(opposite~side)/(adjacent~side)`

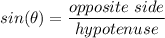
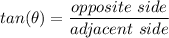
These relationships are often memorized with SoaCahToa, where, the S, C, or T, represent the Sine, Cosine, and Tangent, functions, and the "o", "a", or "h", represent the opposite side, the adjacent side, or the hypotenuse (the side across from the right angle).

Picking up from the diagram, we're trying to find the angle "a", and we know two sides of a right triangle, so we need to identify which trigonometric function uses the two given sides, relative to angle "a".

For angle "a", the 40m distance to the tower is the adjacent side of the triangle (touching both the right angle, and the angle "a"), and the 23.09m tower height is the opposite side (touching the right angle, but not touching the angle "a").

Given that the known sides are "opposite" and "adjacent", we'll need to use the Tangent function:

`\tan(\theta)=(opposite)/(adjacent)`

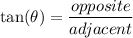
substituting known values...

`\tan(a^o)=((23.09~m))/((40~m))`

simplifying units...

`\tan(a^o)=(23.09)/(40)`

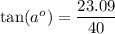
applying arctan to both sides to undo the tangent function, and evaluating ...

`\arctan ( ~tan(a^o)~)=\arctan \left ((23.09)/(40) \right)`

`a^o=\arctan \left ((23.09)/(40) \right)`

`a^o=29.99569...^o`

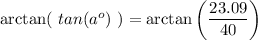
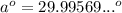
Rounding to the nearest hundredth...

`a^o \approx 30.00^o`

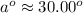
Noting that the problem says that the angle of elevation is "a degrees", so "a" is just a number (without degrees).

`a \approx 30.00^`