Question

Below are two inequalities and the graphs of their without the shading. By imagining where the shading should be, identify which point would satisfy BOTH

inequalities

Answer 1

Answer: C

Explanation:

Answer 2

D. (-2, 10)

Explanation:

Given inequalities:

`y > -(5)/(3)x+2`

`y > 3x+2`

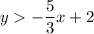
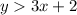
Both inequalities have been given in slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept.

The first equation has a negative slope, which means that as x increases, y decreases. Therefore, it is the dashed line that begins in quadrant II and ends in quadrant IV.

The second equation has a positive slope, which means that as x increases, y increases. Therefore, it is the dashed line that begins in quadrant III and ends in quadrant I.

When graphing inequalities, the inequality sign ">" indicates a dashed line and shading above the line.

As both inequalities should be shaded above the lines, the region where the shaded regions overlap is the upper "V" of the graph (see attachment).

A point that satisfies both inequalities is any point that is located in the overlapping shaded region, but not found on the dashed lines.

Therefore, the point that satisfies both inequalities is (-2, 10).