Question

From the point A (1,-2), a perpendicular is drawn to the line 2x + 3y = 9 to meet it at M. Find the

coordinates of M and the length of AM.

Answer 1

Answers:

• M = (3,1)
• Segment AM is exactly
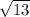  `√(13)` units long. That approximates to 3.605551 units.

================================================

Step-by-step explanation:

The standard form for linear equations is Ax+By = C. Anything perpendicular to this would be of the form Bx-Ay = D.

The equation 2x+3y = 9 gives

• A = 2
• B = 3
• C = 9

The perpendicular template goes from Bx-Ay = D to 3x-2y = D.

Plug in the coordinates of (1,-2) to compute D.

3x-2y = D

D = 3x-2y

D = 3*1 - 2*(-2)

D = 7

Therefore, the perpendicular equation is 3x-2y = 7

-----------------------

We need to solve this system

`\begin{cases}2x+3y = 9\\3x - 2y = 7\end{cases}`

to locate point M.

There are a few methods. I'll use substitution.

Solve the 1st equation for x.

2x+3y = 9

2x = -3y+9

x = (-3y+9)/2

x = -1.5y + 4.5

Then substitute this into the other equation to solve for y.

3x - 2y = 7

3( x ) - 2y = 7

3( -1.5y+4.5 ) - 2y = 7

-4.5y + 13.5 - 2y = 7

-6.5y + 13.5 = 7

-6.5y = 7-13.5

-6.5y = -6.5

y = -6.5/(-6.5)

y = 1

Use that to determine x.

x = -1.5y + 4.5

x = -1.5*1 + 4.5

x = 3

Point M is located at (x,y) = (3, 1)

------------------------

Use the distance formula to find the distance from A(1,-2) to M(3,1)

`A = (x_1,y_1) = (1,-2) \text{ and } M = (x_2, y_2) = (3,1)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((1-3)^2 + (-2-1)^2)\\\\d = √((-2)^2 + (-3)^2)\\\\d = √(4 + 9)\\\\d = √(13)\\\\d \approx 3.605551\\\\`

Segment AM is exactly
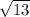`√(13)` units long.

That is approximately 3.605551 units.

You can use a tool like GeoGebra to confirm the answers are correct.