Answer:
(a) -
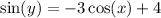
(b) -
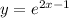
Explanation:
Given the two part question...
(a) - Solve the following first-order differential equation with the given initial condition.

(b) - Given that y=f(x) passes through the point (1,e) and has the property that the slope of the tangent line to the graph at any point "P" is equal to twice the y-coordinate of "P." Find f(x).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Part (a) -
The given DE is a separable differential equation and can be solved in the following manner.
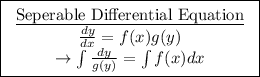

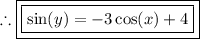
Thus, the DE is solved.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Part (b) -


Use the given initial condition to find "C." y(e)=1


Thus, f(x) is found.