Answer:
17.6 years (roughly)
Explanation:
ok so let's consider the amount of cobalt-60 to be:
 kg of cobalt.
kg of cobalt.
We can model the decay of that cobalt given its half-life of
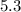 as:
as:
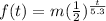
where
 is the time in years.
is the time in years.
Now, for 90% of the cobalt to decay, we get the following equation:
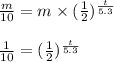
and by using logarithms, we can find t.
![log((1)/(10))=log((1)/(2)^(t)/(5.3))\\ \\ log(1)-log(10)=(t)/(5.3) log((1)/(2))\\\\(log(1)=0)\\\\ -log(10)=(t)/(5.3) [log(1)-log(2)]\\\\(log[10]=1) \\\\](https://img.qammunity.org/2024/formulas/mathematics/high-school/qpes8wjgy6ytglu25g1r0s3aou1z45qdnr.png)
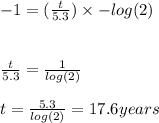 (roughly)
(roughly)