Question

In an experiment, two protons are shot directly toward each other, each moving at half the speed of light relative to the laboratory.a What speed does one proton measure for the other proton?b What would be the answer to part (a) if we used only nonrelativistic Newtonian mechanics?c What is the kinetic energy of each proton as measured by an observer at rest in the laboratory?d What is the kinetic energy of each proton as measured by an observer riding along with one of the protons?e what would be the answers to part (c) if we used only nonrelativistic Newtonian mechanics?f What would be the answers to part (d) if we used only nonrelativistic Newtonian mechanics?

Answer 1

Each proton sees the other moving at a relativistic speed of 0.8c, not 1c due to the relativistic velocity addition. Kinetic energy is calculated differently in relativistic terms compared to nonrelativistic Newtonian mechanics, which would provide incorrect values at these high speeds.

Step-by-step explanation:

a. Relative speed of one proton as measured by the other:

The relative speed between the two protons can be calculated using the relativistic velocity addition formula:

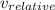`v_{relative` = (v₁ + v₂) / (1 + v₁ × v₂ / c²)

where:

v₁ and v₂ are the velocities of the protons relative to the laboratory (half the speed of light, or c/2)

c is the speed of light

Plugging the values and solving for
`v_{relative`:

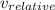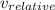`v_{relative`= (c/2 + c/2) / (1 + (c/2) × (c/2) / c²) = 0.8c

Therefore, each proton measures the other proton moving at 0.8 times the speed of light.

b. Relative speed using Newtonian mechanics:

If we used Newtonian mechanics, which is valid for speeds much smaller than the speed of light, the relative velocity would simply be the sum of the individual velocities:

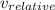`v_{relative`= v₁ + v₂ = c/2 + c/2 = c

However, this is incorrect due to the effects of special relativity, which become significant at high velocities.

c. Kinetic energy as measured in the laboratory:

The kinetic energy of each proton as measured by an observer in the laboratory can be calculated using the relativistic formula:

KE = mc² × ((1 - v²/c²)
`^{(-1/2)`
`^ {- 1)`

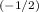
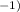
where:

m is the mass of a proton (1.6726219e-27 kg)

v is the velocity of the proton (c/2)

c is the speed of light

Plugging the values and solving for KE:

KE = 1.6726219e-27 kg × (3e8 m/s)² × ((1 - (c/2)²/c²)
`^{(-1/2)`
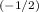
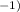`^ {- 1)` = 6.71e-11 J

Therefore, each proton has a kinetic energy of approximately 6.71e-11 J as measured in the laboratory.

d. Kinetic energy as measured by a co-moving observer:

An observer riding along with one of the protons would be in the proton's rest frame. In this frame, the proton is at rest, and therefore has zero kinetic energy.

e. Non-relativistic kinetic energy in the lab:

Using the non-relativistic kinetic energy formula:

KE = 1/2 × mv²

we get:

KE = 1/2 × 1.6726219e-27 kg × (c/2)² ≈ 4.14e-11 J

This is less than the relativistic kinetic energy, which is expected as relativity predicts an increase in kinetic energy at high velocities.

f. Non-relativistic kinetic energy in the co-moving frame:

Similarly, in the co-moving frame, the non-relativistic kinetic energy of the proton would be:

KE = 1/2 × mv² = 0

This is consistent with the fact that the proton is at rest in this frame.