Question

To create a square snowflake, use the following steps. (See figure below.) 1. Draw a square. 2. Divide each of the square's straight lines into fourths. In a clockwise order: • Leave the first fourth alone. • Replace the second fourth with a square that's on the outer side of the line. • Replace the third fourth with a square that's on the inner side of the line. . • Leave the last fourth alone. Apply the above procedure to each of the square's straight lines. Be sure to do the above in a clockwise order! 3. Apply the procedure from step 2 to each of the straight lines in step 2. 4. Apply the procedure from step 2 to each of the previous step's straight lines. Continue this process indefinitely. (a) Find a formula for the total perimeter P of step n of the process described above if the original square has sides of length 1 ft. P_n =____ ft (b) Use the formula from part (a) to find the perimeter of a square snowflake. (Enter INFINITY for co if needed.) P=____ ft (c) Find a formula for the total area A of step n of the above process if the original square has sides of length 1 ft. HINT: It's an incredibly easy formula. Don't make it hard. A_n =____ sq ft (d) Use the formula from part (c) to find the area of a square snowflake. (Enter INFINITY for co if needed.) A =____sq ft

Answer 1

To create a square snowflake, use the following steps. (See figure below.) 1. Draw a square. 2. Divide each of the square's straight lines into fourths. In a clockwise order: • Leave the first fourth alone. • Replace the second fourth with a square that's on the outer side of the line. • Replace the third fourth with a square that's on the inner side of the line. . Leave the last fourth alone. Apply the above procedure to each of the square's straight lines. Be sure to do the above in a clockwise order! 3. Apply the procedure from step 2 to each of the straight lines in step 2. 4. Apply the procedure from step 2 to each of the previous step's straight lines. Continue this process indefinitely. step 1 15 Dividing the lines into fourths Replacing the 2nd and 3rd fourths on the top line Replacing the 2nd and 3rd fourths on two lines Replacing the 2nd and 3rd fourths on all lines step 2 (a) Find a formula for the total perimeter P of step n of the process described above if the original square has sides of length 1 ft. Po = ft (b) Use the formula from part (a) to find the perimeter of a square snowflake. (Enter INFINITY for co if needed.) P= ft (c) Find a formula for the total area A of step n of the above process if the original square has sides of length 1 ft. HINT: It's an incredibly easy formula. Don't make it hard. A = sq ft (d) Use the formula from part (c) to find the area of a square snowflake. (Enter INFINITY for co if needed.) A = sq ft

Explanation:

Answer 2

The total perimeter of the square snowflake can be expressed as
`Pn = 4 * (4/3)n`. As n approaches infinity, the perimeter becomes infinite. For the total area, it follows a geometric series and converges to a finite limit,
`A = 1/(1 - (3/4)^2).`

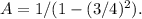
To find a formula for the total perimeter Pn of step n in the square snowflake construction process, identify the pattern of perimeter growth. Let's begin with a square of side length 1 ft:

At step 0, the perimeter P0 is 4 ft (since it's simply a square with sides of length 1 ft).

At step 1, each side of the original square is divided into fourths, creating a pattern that adds 3 segments for every 4 segments of the original side. Thus, the perimeter is multiplied by 4/3 for each of the four sides, giving P1 = P0 * (4/3) * 4.

For step n, you repeat this process n times, leading to the formula Pn = P0 * (4/3)n * 4.

Since P0 = 4, we get Pn = 4 * (4/3)n.

For part (b), as n approaches infinity, the perimeter will grow indefinitely, and the perimeter P approaches infinity.

Part (c) asks for the formula for total area An of step n. Each square added increases the area by a constant amount:

The area added in each step is the area of one side of the preceding square squared. Since the side length after each step is divided by 4, the new square adds an area that is (1/4)2 of the side's length squared.

With 8 new squares added per step, the total area can be calculated by summing the area added at each step. This leads to the series An = 1 + 8 * (1/4)2 + 8 * (1/4)2 * (3/4)2 + ..., up to n terms.

This is a geometric series with a common ratio r = (3/4)2, and the formula becomes An = 1 * (1 - rn)/(1 - r).

In part (d), as n reaches infinity, the added area gets infinitesimally small, and the series converges to a finite limit. Therefore, the total area A is finite and equals A = 1/(1 - (3/4)2).