Answer:
1 = (x/11)² +24y²/605
Explanation:
You want the the equation of an ellipse through the point (1, 5) with ends of its major axis at (±11, 0).
Ellipse equation
The ellipse equation will have the form ...
(x/11)² + (y/b)² = 1
for some value 'b' that causes (x, y) = (1, 5) to be a solution to this equation.
Value of b
Using the given point and solving for b (or b²), we have ...
(1/11)² +(5/b)² = 1
25/b² = 1 -1/121 = 120/121
Inverting this equation and multiplying by 25, we have ...
b² = 605/24
Equation of interest
Using this value for b², we can write the equation of the ellipse as ...
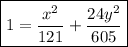
<95141404393>