Question

(question 15) Find the derivative of the function
using logarithmic differentiation.

Answer 1

`\textsf{A.} \quad (2+x)^x\left[(x)/(2+x)+\ln(2+x)\right]`

Explanation:

Replace f(x) with y in the given function:

`y=(x+2)^x`

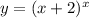
Take natural logs of both sides of the equation:

`\ln y=\ln (x+2)^x`

`\textsf{Apply the log power law to the right side of the equation:} \quad \ln a^n=n \ln a`

`\ln y=x\ln (x+2)`

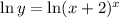
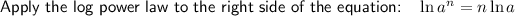
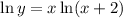
Differentiate using implicit differentiation.

Place d/dx in front of each term of the equation:

`\frac{\text{d}}{\text{d}x}\ln y=\frac{\text{d}}{\text{d}x}x\ln (x+2)`

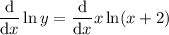
First, use the chain rule to differentiate terms in y only.

In practice, this means differentiate with respect to y, and place dy/dx at the end:

`(1)/(y)\frac{\text{d}y}{\text{d}x}=\frac{\text{d}}{\text{d}x}x\ln (x+2)`

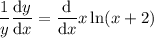
Now use the product rule to differentiate the terms in x (the right side of the equation).

`\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\frac{\text{d}y}{\text{d}x}=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}$\\\end{minipage}}`

`\textsf{Let}\; u=x \implies \frac{\text{d}u}{\text{d}x}=1`

`\textsf{Let}\; v=\ln(x+2) \implies \frac{\text{d}v}{\text{d}x}=(1)/(x+2)`

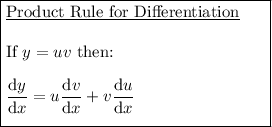
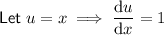
Therefore:

`\begin{aligned}(1)/(y)\frac{\text{d}y}{\text{d}x}&=x\cdot (1)/(x+2)+\ln(x+2) \cdot 1\\\\(1)/(y)\frac{\text{d}y}{\text{d}x}&= (x)/(x+2)+\ln(x+2)\end{aligned}`

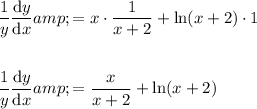
Multiply both sides of the equation by y:

`\frac{\text{d}y}{\text{d}x}&=y\left( (x)/(x+2)+\ln(x+2)\right)`

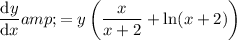
Substitute back in the expression for y:

`\frac{\text{d}y}{\text{d}x}&=(x+2)^x\left( (x)/(x+2)+\ln(x+2)\right)`

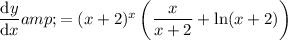
Therefore, the differentiated function is:

`f'(x)=(x+2)^x\left[(x)/(x+2)+\ln(x+2)\right]`

`f'(x)=(2+x)^x\left[(x)/(2+x)+\ln(2+x)\right]`