Question

(question 8) Find the critical points of the function

Answer 1

`\textsf{A.} \quad (-3)/(2)`

Explanation:

The critical points of a function are the points where the derivative of the function is either zero or undefined.

We can find the derivative of the given function using the product rule.

`\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\frac{\text{d}y}{\text{d}x}=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}$\\\end{minipage}}`

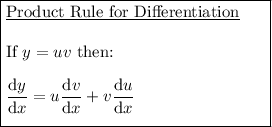
Given function:

`f(x)=(2x+1)e^x`

`\textsf{Let}\; u=2x+1 \implies \frac{\text{d}u}{\text{d}x}=2`

`\textsf{Let}\; v=e^x \implies \frac{\text{d}v}{\text{d}x}=e^x`

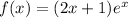
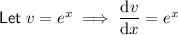
Apply the product rule:

`\begin{aligned}f'(x)&=(2x+1)e^x+e^x(2)\\&=(2x+1)e^x+2e^x\\&=e^x(2x+1+2)\\&=e^x(2x+3)\end{aligned}`

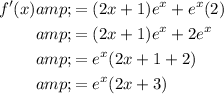
Set the derivative equal to zero and solve for x:

`\begin{aligned}f'(x)&=0\\e^x(2x+3)&=0\\2x+3&=0\\2x&=-3\\x&=-(3)/(2)\end{aligned}`

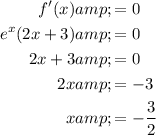
Therefore, the critical point of the function f(x) is when x = -3/2.