Write an equation for a sine function which has a minimum of -9, a maximum of 3, a period of 2pi and is shifter 0.5 units to the right

Question

asked Feb 9, 2024 97.8k views

1 Answer

Andrew Sawa · Answer 1 · 2024-02-15T21:32:24+0000

Answer:

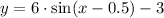
$y=6\cdot \sin(x-0.5)-3$

Step-by-step explanation:

For the equation:

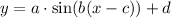$y=a\cdot \sin(b(x-c))+d$ ...

As
|a| increases, the wave’s amplitude increases.

As
increases, the wave’s period (wavelength) decreases.

$\text{period} = (2\pi)/(b)$

As
increases, the wave shifts to the right. (horizontal/phase shift)

As
increases, the wave shifts upwards. (vertical shift)

We can solve for the amplitude of the given sine function by finding half the difference of its minimum and maximum y-values.

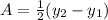
A=(1)/(2)(y_2 - y_1)

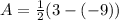
A=(1)/(2)(3 - (-9))

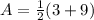
$A=\frac{1}2(3 + 9)$

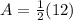
$A=\frac{1}2(12)$

A=6

This means that in the above equation (
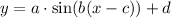$y=a\cdot \sin(b(x-c))+d$ ),

a = A = 6 .

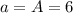We know that
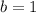b=1 because the period is
$2\pi$ .

We know that
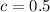c=0.5 because the wave is shifted 0.5 units to the right.

We can find the vertical shift (
) by adding the amplitude to the minimum y-value to get the center y-value of the function.

d= -9 + 6

d = -3

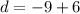
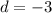
Finally, we can put these variables together to form the equation:

$\boxed{y=6\cdot \sin(x-0.5)-3}$